Boîtes

Identification

Rallye: 17.I.05 ; catégories: 3, 4, 5 ; domaine: 3D
Familles:

• VS - Visualiser dans l'espace
• VS/SV - Traiter des développements de solides

Remarque et suggestion

Résumé

Déterminer le nombre de parallélépipèdes que l'on peut construire à l'aide d'une famille de rectangles représentant les faces.

Enoncé

Tâche de résolution et savoirs mobilisés

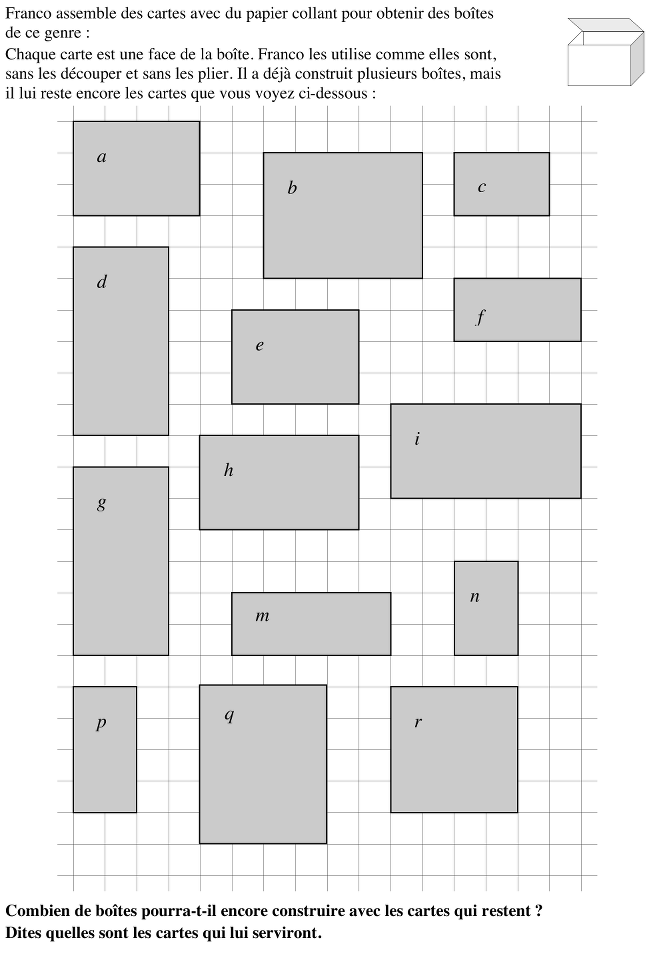
Extraits de l'analyse a posteriori de ce problème: (Voir article en bibliographie)

Pour résoudre ce problème, il faut faire appel à un grand nombre de connaissances:

1. Il faut savoir combien de faces a un parallélépipède.

2. Il faut savoir que les faces opposées sont isométriques.

3. Il faut être capable d’extraire les longueurs des côtés de chacune des faces de leurs représentations en deux dimensions (passage du bidimensionnel à l’unidimensionnel).

4. Et surtout il faut être capable d’imaginer comment les faces se juxtaposeront les unes avec les autres dans le passage du bidimensionnel au tridimensionnel (ou d’avoir de bonnes capacités de manipulation et de reconstruction).

La familiarité des enfants avec les boîtes de différentes formes n’assure pas que toutes ces connaissances soient acquises.

Notions mathématiques

rectangle, parallélépipède, vision spatiale, face, volume, solide, plan, espace à trois dimensions

Résultats

17.I.05

Points attribués sur 1207 classes de 21 sections:

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: La boîte correctement reconstruite ou désignée (a, c, e, f, n, p), avec l’affirmation qu’il n’est pas possible de former une autre boîte et une explication complète qui se réfère aux longueurs des côtés et à l’égalité des rectangles
• 3 points: La boîte correctement reconstruite ou désignée et l’affirmation de l’unicité, avec explication incomplète ou peu claire
  ou la boîte correctement reconstruite ou désignée avec explications mais sans allusion à l’unicité
• 2 points: La boîte correctement reconstruite ou désignée, sans aucune explication
• 1 point: Début de raisonnement dans lequel les rectangles égaux sont regroupés par deux, mais ne peuvent pas s’alterner correctement
• 0 point: Incompréhension du problème

Procédures, obstacles et erreurs relevés

Une analyse détaillée des copies a permis de constater que la procédure la plus efficace est le découpage des figures proposées puis leur juxtaposition deux à deux.

Dans plusieurs cas il est fait référence aux mesures des côtés, par comptage des carrés du quadrillage ou par utilisation de la règle graduée. Cette procédure a permis l'exclusion des rectangles qui ne sont pas appariés (pas égaux à un autre). L’identification des faces a permis la construction ou le dessin de l'unique boîte possible. La représentation qui correspond aux meilleurs résultats est le développement dans le plan (patron) pour 30% des copies, alors que seulement le 15% présentent un dessin à trois dimensions. Ces données sont à peu près les mêmes dans chacune des trois catégories. On relève 15% de copies blanches, avec une légère diminution de la catégorie 3 à la catégorie 5.

La difficulté de reconnaître les rectangles égaux est très fréquente. L'utilité ou la nécessité de prendre en compte les mesures correctes des côtés des rectangles afin de construire la boîte ou de l'identifier n'a pas été ressentie.

Les appariements de rectangles n'ont pas toujours conduit à la reconstruction de la boîte, à la suite d'erreurs de mesures. On a relevé des essais de boîtes avec 5 faces ou d'utilisation de 10 rectangles pour le développement d'une boîte. L’absence d'une vision tridimensionnelle de l’objet est très fréquente : difficulté de passer du plan à l'espace, en raison d'erreurs d'assemblage et/ou de prise en compte des caractéristiques géométriques des figures proposées .

On a aussi relevé des cas d'application de raisonnements arithmétiques complètement dissociés de la vision géométrique. Par exemple 14:6= 2,2 avec la conviction de pouvoir construire deux boîtes avec un reste de deux pièces, en ignorant complètement, encore une fois, les contraintes des caractéristiques géométriques à prendre en compte.

L'utilisation de lettres minuscules pour désigner les pièces a entraîné des confusions entre les lettres b et q et entre p et d. Dans d'autres cas la même pièce a été utilisée plusieurs fois, sans respecter la consigne et dans d'autres cas encore les pièces ont été modifiées pour les adapter afin de "fermer" ou compléter la boîte.

(Pour plus e détails, voir l'article en bibliographie)

Exploitations didactiques

Le problème se révèle ambitieux pour des élèves d'école primaire, en particulier pour ceux des catégories 3 et 4 (insuccès de 70% et 80%).

Il est évident que la capacité de visualiser mentalement les objets en trois dimensions et de savoir passer du plan à l'espace et réciproquement est requise. Il faut en outre savoir lire les mesures avec les unités suggérées (celles du quadrillage) mais que tous ne perçoivent pas et n'exploitent pas, au point tel que de nombres élèves déclarent qu'après avoir découpé les pièces ils utilisent la règle pour en mesurer les côtés égaux.

A la lumière de ces résultats on peut suggérer de commencer tôt, puis d'intensifier le nombre d'expériences au travers desquelles l'élève puisse manipuler des objets réels, comme les boîtes, pour ensuite pouvoir en reconnaître par une représentation plane, les parties dont ils sont composés (les faces). Ceci est fondamental si l'on pense aux copies où les boîtes ont 5 ou 7 faces où à celles où des faces sont bien recopiées/dessinées sur la feuille mais dans une disposition complètement erronée pour la reconstruction effective de la boîte elle-même.

Si le problème est très difficile pour une classe de catégorie 3, il convient cependant pour des classes de catégories 4 et 5 comme approche de l'étude du parallélépipède rectangle.

Pour aller plus loin

Le même problème a été expérimenté avec des élèves de première année d'école secondaire (categorie 6). Les résultats obtenus, même s'ils sont peu significatifs au vu du nombre limité de copies (18 groupes de 3/5 élèves, c'est-à-dire un échantillon de 70-80 élèves) correspondent tout à fait à ceux obtenus en catégorie 4 ( moyenne 1,07 ). Les conditions de passation étaient un travail par groupes de 3 à 5 élève, sur une durée de 25 minutes. En voici les résultats :

2 groupes, 11%, résolvent le problème et donnent les explications (3 et 4 points),

3 groupes, 17%, résolvent le problème sans donner d'explications (2 points,

7 groupes, 39%, montrent un début de raisonnement (1 point), construisent une boîte mais avec des pièces incorrectes,

6 groupes, 33%, ne comprennent pas le problème (0 point), même s'il ont fait quelque chose: 3 groupes ont construit 2 boîtes, les 3 autres ont construit des boîtes avec 5 ou 10 faces.

A la lumière de ces résultats il paraît évident que pour chercher à améliorer cette situation il faut travailler dès les premières années de l'école primaire en géométrie à trois dimensioni et, surtout, par manipulations et constructions de modèles d'objets. Ces activités devront être reprises à l'école secondaire pour créer une continuité de travail qui évite chez les élèves les conflits entre images mentales et concepts géométriques (voir V. Villani, Geometria dello spazio, L’insegnamento della matematica e delle scienze integrate, vol.10,n°5). Il est aussi indispensabile que la période de transition de la manipulation d'objets ou modèles à la "mathématisation" ou à l'abstraction se déroule dans les temps nécessaires et adéquats permettant la maturation complète de cette phase.

Bibliographie

G. Telatin, 2015, Ripartiamo da... 0 punti / Repartons du 0 point In. La Gazzetta di Transalpino / La Gazette de Transalpie, no 4, 2015, pp 95-114

(c) ARMT, 2009-2024