Il plastico

Identificazione

Rally: 19.II.11 ; categorie: 5, 6, 7, 8 ; ambito: 3D
Famiglie:

• VS - Visualizzare nello spazio
• VS/2D - Cambiare il punto di vista

Remarque et suggestion

Sunto

Riconoscere e correlare le rappresentazioni di due diverse proiezioni prospettiche della stessa struttura solida e calcolare il numero di elementi richiesti.

Enunciato

Compito per la risoluzione e saperi mobilizzati

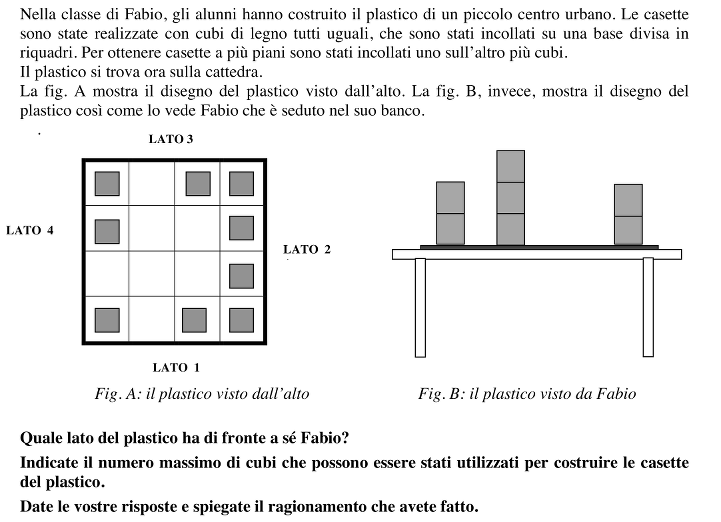
Capire quale lato del plastico ha di fronte a sé Fabio facendo riferimento alla Fig. A. Osservare il plastico mettendosi ogni volta di fronte a ciascuno dei suoi lati, confrontando ciò che si immagina di poter vedere con ciò che è disegnato in Fig. B. Oppure è possibile ruotare il foglio in modo da guardare il plastico di Fig. A avendo di fronte ogni volta uno dei lati. Dedurre che Fabio non può aver di fronte il LATO 1 del plastico, perché altrimenti in Fig. B le case affiancate dovrebbero essere a destra e non a sinistra; non può avere di fronte il LATO 4, né il LATO 2, perché altrimenti vedrebbe una casa anche nello spazio vuoto di Fig. B. Rendersi conto che solo dal LATO 3 Fabio può vedere il plastico così come appare nel disegno di Fig. B.

Ricavare il numero massimo di cubi utilizzabili nella costruzione delle casette, partendo dalla Fig. B. Considerare che, in essa, cominciando dalla sinistra di chi guarda, si vedono due cubi, quindi 2 è il massimo numero di cubi per ogni casetta che si trova nella corrispondente fila del plastico di Fig. A (le casette sono 4, perché tutte e 4 le caselle a destra in Fig. A sono occupate).

Spostarsi verso destra in Fig. B: individuare 3 come numero massimo di cubi per ogni casetta, che si trova nella corrispondente fila del plastico (le casette sono 2, perché 2 caselle sono occupate in Fig. A).

Spostandosi ulteriormente a destra nella Fig. B si vedono ancora 2 cubi, e quindi 2 è il massimo numero di cubi per ogni casetta che si trova nella corrispondente fila del plastico (le casette sono 3, perché 3 sono le caselle occupate a sinistra in Fig. A).

Calcolare il numero massimo di cubi: (2 x 4) + (3 x 2) + (2 x 3) = 20.

Saperi mobilizzati: per risolvere adeguatamente il problema occorre padroneggiare la lateralizzazione dello spazio (distinzione destra/sinistra) ed essere in grado di osservare e riconoscere punti di vista diversi di uno stesso oggetto.

Nozioni matematiche

punti di vista, visione dall’alto, visione laterale, corrispondenza tra piane i spazio

Risultati

19.II.11

Su 411 protocolli esaminati delle sezioni di Siena, Rozzano, Milano e Riva i punteggi attribuiti sono stati i seguenti:

Confrontando i valori delle medie sopra riportate con i risultati conseguiti dalle 2553 classi provenienti da tutte le 20 sezioni , si osserva che i valori non si discostano in modo significativo avendo una differenza in più o meno compresa fra lo 0,2 e lo 0,3.

Secondo i criteri dell’analisi a priori:

• 4 Risposte corrette (LATO 3; numero massimo di cubi: 20) con spiegazione chiara del ragionamento
• 3 Risposte corrette con spiegazione poco chiara oppure indicazione corretta solo del numero massimo di cubi con spiegazione del procedimento
• 2 Risposte corrette senza spiegazione
• 1 Solo la determinazione corretta del punto di vista (LATO 3)
• 0 Incomprensione del problema

Osservando i dati della tabella si nota che passando da cat. 5 (1,6) a cat. 8 (3,1) c’è un incremento rilevante del valore medio dei punteggi, che aumenta sempre passando a categorie superiori. Gli insuccessi (punteggi 0 e 1) e fra questi solo il 4% di Cat.5 e il 3% di Cat.6 hanno consegnato il foglio in bianco, sono il 55% in Cat.5, il 36% in Cat.6, il 21% in Cat.7 e il 14% in Cat.8. Lo stesso discorso vale per i successi (punteggi 3 e 4), ovviamente a parti invertite, che parte da Cat.5 con il 31% per arrivare gradualmente al 79% di Cat.8.

Questo aspetto per cui aumentando l’età dei ragazzi le prestazioni migliorano ci può far pensare che più esperienze adatte e coinvolgenti fanno più riescono a costruire quest’abilità di visualizzazione.

Procedure, ostacoli ed errori rilevati

Per la scelta del punto di vista del lato sono state utilizzate in tutte le categorie le seguenti strategie : nella maggior parte dei casi gli elaborati riportano l’esclusione dei punti di vista non adeguati con argomentazione; molti elaborati evidenziano la rotazione delle due figure con il confronto delle stesse; utilizzo di modelli concreti per organizzare lo spazio. Per individuare il numero massimo di cubi si collegano, o per rotazione o per sovrapposizione, le due figure, quindi si conta il numero dei cubetti; costruzione di modelli concreti secondo le indicazioni date dalla figura B, confrontata con la figura A; rappresentazione grafica dei cubi visti dall’alto, conteggiati fila per fila; soluzioni aritmetiche date dal conteggio fila per fila, senza disegno.

(figure Elaborato 08032)

Per la categoria 5, nella scuola primaria, è predominante la strategia con disegno o con manipolazione, mentre nelle categorie 7, 8 prevale la strategia algebrica, ovvero ragionamento e rappresentazione con numeri. Quest’analisi deriva dall’osservazione degli elaborati che hanno ottenuto punteggi 3 o 4, quindi con entrambe le risposte corrette.

Gli elaborati con punteggio 2 sono poco numerosi e statisticamente non significativi, perché rispecchiano i criteri di attribuzione dei punteggi.

Rispetto al primo quesito, in categoria 5 l’errore più frequente è la scelta del lato 4, che evidenzia la correttezza della lateralità, ma che non tiene conto della visione prospettica. Nelle categorie successive questo errore è meno frequente, fino a scomparire in categoria 8. Altro errore, anche se meno frequente, è la scelta del lato 1 che testimonia ancora qualche problema di lateralità non risolto. Tale errore non è presente negli elaborati di cat. 6 e successive.

Secondo quesito: risposte errate più frequenti

• 3 dovuto alla confusione fra il numero massimo di piani di una casetta con il numero massimo di cubi che possono essere utilizzati per costruire tutte le casette;
• 27 (3 x 9) derivante dalla confusione fra il numero massimo di piani e il numero di disposizioni possibile dei cubetti (9)
• 21 (7 x 3) determinato dal conteggio dei cubi presenti nella figura B (7) e il numero di file presenti (3) o il numero di piani
• 16 o 48 derivante dal numero di caselle presenti nel disegno (16) o dal numero di caselle presenti moltiplicato per 3 , che è il numero massimo di piani

Sono anche presenti errori del tipo

• 63 dato, dal conteggio dei cubi della figura B , che sono 7, moltiplicati per 9 che sono la disposizione dei cubi della figura A
• 29 (4 x 7 = 28; 28 + 1 = 29) determinato dal numero di cubetti visibili nella figura B (7), moltiplicato per 4, ovvero il numero dei lati, più il cubetto in più del lato 4.

Questi errori rivelano che l’ostacolo essenziale del problema per i ragazzi più giovani è il seguente : essi vedono 9 quadrati su una figura, 7 sull’altra, ma non vedono quelli che sono nascosti perché non sono ancora capaci di interpretare le figure come proiezioni ortogonali.

Indicazioni didattiche

Il problema permette un buon approccio alla “visualizzazione spaziale”, alle differenti proiezioni di un oggetto , anche in relazione con altre discipline come la geografia o con le attività manuali di costruzione di modelli a 3 dimensioni.

Nella versione attuale, il problema non è molto interessante per i ragazzi di cat.7 e 8, poiché la maggior parte trova delle buone risposte ( i successi sono dell’ordine 60-80% ). Si potrebbe farlo oggetto di sviluppi ulteriori : in cat.5 e 6 e persino con ragazzi più giovani,l’attività è più pertinente perché permette ai ragazzi di confrontarsi con una problematica nuova : la comparazione di un oggetto a 3 dimensioni con rappresentazioni a 2 dimensioni. L’attività di risoluzione deve sfociare nella validazione o nella messa in comune di quello che essi non possono capire senza manipolazione o costruzione effettiva. I ragazzi devono poter costruire un modello ( con un semplice assemblaggio di cubi) secondo le figure A e B. Essi devono poter toccare i cubi, spostarli, girare attorno al modello o farlo girare. E’ solamente quest’attività sperimentale che permette loro di comprendere che

la fig. A ci dà la posizione delle 9 case , ma non le altezze

la fig. B dà solo l’altezza della più alta delle case di una fila , ma non il suo posto.

Essi allora constateranno che le 2 figure non corrispondono alla loro visione personale ; vedranno dei cubi ( con parecchie facce) mentre troveranno dei quadrati sulle proiezioni.

Per andare più lontano

L’esperimento scritto sopra necessita di un grande investimento di tempo ( costruzione, sviluppo, confronto che non si può pensare di non utilizzare se vogliamo andare più lontano ) .

Per dominare questa rappresentazione non è sufficiente saper leggere ed interpretare una proiezione. Si potrebbe domandare ai ragazzi di disegnare delle proiezioni del modello da altri punti di vista. Ci si renderà conto allora che le figure A e B non sono sufficienti per definire l’oggetto e che ci sono numerosi modelli conformi ad A e B con case di altezze differenti in posizioni differenti. Si arriva quindi ad approfondire la questione del numero dei cubi . Nel parlare del numero massimo dei cubi si potrebbe domandare :

• trovare il numero minimo di cubi per un modello conforme alle fig. A e B

• individuare quanti sono i modelli differenti

• quanti diversi modelli, sempre conformi ad A e B si potranno costruire con un cubo di meno del numero massimo.

Si può anche verificare l’unicità della costruzione aggiungendo una terza proiezione e un numero dato di cubi. L’attività può diventare così una ricerca potenzialmente interessante.

(c) ARMT, 2011-2024