Pauvre octaèdre

Identification

Rallye: 10.F.16 ; catégorie: 8 ; domaine: 3D
Familles:

• VS - Visualiser dans l'espace
• VS/2D - Changer de points de vue

Envoyer une remarque ou une suggestion

Résumé

Observer les six pyramides déterminées par chaque sommet de l'octaèdre et les quatre points milieux des arêtes adjacentes et décrire le solide qui subsiste lorsqu'on a découpé les six pyramides.

Enoncé

Tâche de résolution et savoirs mobilisés

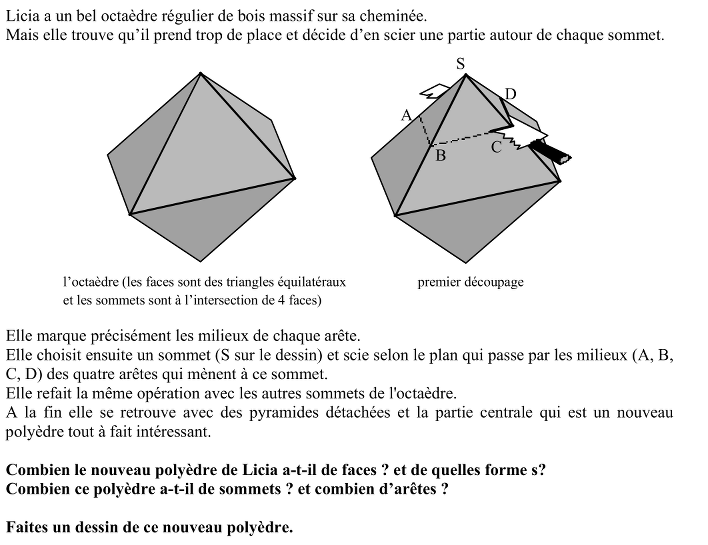
- Imaginer le découpage et la forme des pyramides détachées (à base carrée) ou se construire un tétraèdre et y dessiner les traits de scie sur les faces.

- Imaginer ou dessiner la forme des faces du nouveau polyèdre qui subsistent sur les faces de l’octaèdre (triangles équilatéraux).

- En déduire qu’il y a 14 faces (6 carrés et 8 triangles équilatéraux) , 12 sommets (communs chacun à 2 carrés et 2 triangles, c’est à dire ((8 x 3) + (6 x 4)) / 4) et 24 arêtes (somme des cotés des faces divisé par 2).

- Ou dénombrer faces et sommets.

{{10rmtf_fr-16a|}}

Notions mathématiques

polyèdre, pyramide, octaèdre

Résultats

Les résultats n'ont pas été conservés ou ne sont pas encore disponibles.