Une rencontre virtuelle

Identification

Rallye: 15.F.21 ; catégories: 9, 10 ; domaine: 3D
Familles:

• LAV - Utiliser des longueurs, surfaces et volumes dans l'espace
• LAV/LA - Mesurer ou calculer des longueur et/ou des aires
• VS - Visualiser dans l'espace

Envoyer une remarque ou une suggestion

Résumé

B et C deux points d'une sphère se trouvent sur le même méridien : C à 30° sous l’Équateur et B à 60° au-dessus de l’Équateur. B et A se situent sur le même parallèle mais en des points diamétralement opposés. Comparer les longueurs de l’arc de méridien qui va de B à C et de l’arc de parallèle qui va de B à A.

Enoncé

Tâche de résolution et savoirs mobilisés

Analyse a priori de la tâche:

- Comprendre qu’il faut mesurer et comparer deux arcs de circonférence de rayons différents (respectivement R celui de la Terrr et r celui du parallèle sur lequel se trouvent Bob et Alain)

- Comprendre que les angles des deux arcs sont respectivement 90° et 180° et que le rayon r est la moitié du rayon R (ce qui se déduit des propriétés des triangles rectangles avec des angles de 30° et 60°, voir figure)

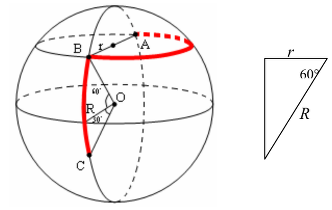
- L’arc de méridien qui va de Bob à Charles est un quart de circonférence de rayon R et l’arc de parallèle qui va de Bob à Alain est une demi-circonférence de rayon R/2. En déduire que la longueur des deux arcs est la même.

Notions mathématiques

sphère, parallèle, méridien, arc de cercle

Résultats

Les résultats n'ont pas été conservés ou ne sont pas encore disponibles.