Navi - bel affichage d'une fiche

Dodécaèdre

Identification

Rallye: 26.I.16 ; catégories: 8, 9, 10 ; domaine: 3D
Familles:

Résumé

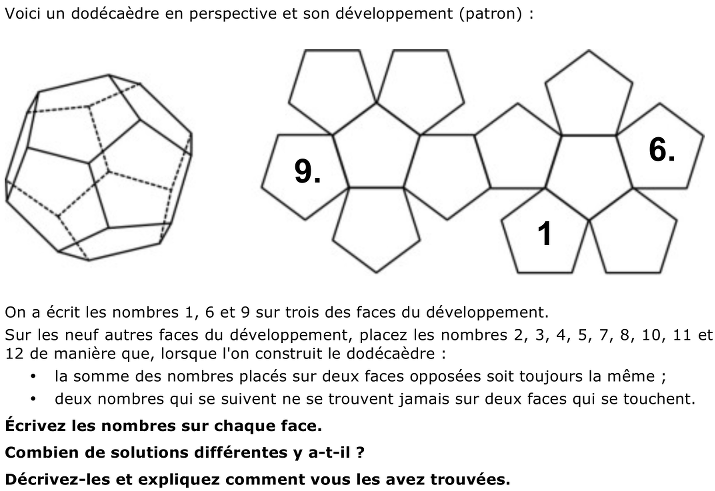
Placer les nombres de 1 à 12 sur les pentagones du développement d'un dodécaèdre de sorte que lorsque le dodécaèdre est construit, la somme des nombres placés sur des faces opposées soit toujours la même et que deux nombres consécutifs ne soient jamais placés sur deux faces adjacentes.

Enoncé

Tâche de résolution et savoirs mobilisés

Analyse a priori de la tâche:

- Déterminer, sur le développement, les faces du dodécaèdre qui sont opposées à 1, 6 et 9, puis les autres paires de faces opposées et aussi les faces qui se touchent.

- Déterminer, que la somme de deux faces opposées est 13, et que : 1 et 12 ; 2 et 11 ; 3 et 10 ; 4 et 9, 5 et 8 ; 6 et 7 sont opposées et marquer les faces 12, 4 et 7 déjà désignées, comme opposées aux faces 1, 9 et 6.

- S’apercevoir que pour les trois paires de faces restantes, il y a plusieurs possibilités qui respectant la deuxième contrainte sur les faces adjacentes.

- Éliminer les nombres à exclure pour les faces déjà notées et procéder par essais et vérifications.

Par exemple à droite du 9 et du 12, ne peuvent être essayés que les nombres 2, 3, 5 (8, 10 et 11 étant éliminés comme voisins) qui correspondraient aux placements respectifs de 11, 10, et 8 sur la face à droite du 4.

En essayant 2 (et 11), il n’y a plus qu’une place pour 3, au-dessous de 11 et 6 et une seule pour 5 (sous le 2).
En essayant 3, on arrive à une impasse.
En essayant 5, on trouve deux dispositions.

- Vérifier que les solutions trouvées respectent tous les critères et sont bien différentes.

Notions mathématiques

dodécaèdre, développement

Résultats

26.I.16

Points attribués sur 1181 classes de 17 sections:

Catégorie	0	1	2	3	4	Nb. de classes	Moyenne
Cat 8	446 (57%)	167 (21%)	139 (18%)	21 (3%)	7 (1%)	780	0.69
Cat 9	101 (49%)	53 (26%)	33 (16%)	11 (5%)	8 (4%)	206	0.89
Cat 10	79 (41%)	51 (26%)	53 (27%)	9 (5%)	3 (2%)	195	1.01
Total	626 (53%)	271 (23%)	225 (19%)	41 (3%)	18 (2%)	1181	0.78
Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème.

Selon les critères déterminés lors de l’analyse a priori :

4 points: Les 3 solutions correctes sont données, sans solution supplémentaire erronée ni doublons avec des explications claires de la procédure suivie (somme 13, placement de 12, 7 et 4, mention des essais, reconnaissance de l’exhaustivité, …)
3 points: Les 3 solutions correctes sont données, sans solution supplémentaire erronée ni doublons, avec explications très partielles (on a fait des essais, …)
ou 2 solutions correctes sont données, sans solution supplémentaire erronée, avec explications claires
2 points: Les 3 solutions correctes sont données mais sans aucune explication
ou 2 solutions correctes sont données, sans solution supplémentaire erronée, avec explications très partielles
ou 2 solutions correctes avec explications, mais avec une solution erronée ou un doublon
ou 1 solution correcte, sans solution supplémentaire erronée et avec explications claires
1 point: 1 solution correcte mais sans aucune explication ou avec explications peu claires
ou 1 solution incomplète (au minimum les nombres 4, 7 et 12 sont correctement placés) avec explications très partielles
0 point: Incompréhension du problème

Banque de problèmes du RMT