
Banca di problemi del RMT
3d62-it
 |
Banca di problemi del RMT3d62-it |
|
Calcolare quante scatole a forma di parallelepipedo rettangolo di dimensioni esterne 8 x 3 x 5 cm, possono essere sistemate in uno scatolone a forma di parallelepipedo rettangolo di dimensioni interne, 60 x 60 x 5 cm.

- Immaginare il compito di riempimento dello scatolone con le scatole piccole in modo da metterne il più possibile o di lasciare il minor spazio vuoto possibile. Un eventuale calcolo del rapporto dei due volumi permette di sapere che il «massimo teorico» è 150 = 18000/120 (o 3600/24 dopo semplificazione per 5) piccole scatole nella grande, per poter valutare le risposte successive trovate.
- Rendersi conto che le scatole piccole possono essere disposte con 8 cm, 5 cm o 3 cm in altezza sul fondo dello scatolone 60 × 60; che la prima disposizione non è possibile perché uscirebbe dallo scatolone, che la disposizione con 3 cm in altezza lascerebbe dei vuoti di 2 cm che non si potrebbero colmare e che bisognerà adottare la disposizione di 5 cm in altezza per una utilizzazione ottimale dello spazio. Il problema si riduce allora nel trovare una disposizione ottimale delle facce rettangolari di 3 × 8 sul «fondo» quadrato dello scatolone 60 × 60.
- Disporre 20 rettangoli di larghezza 3 gli uni di fianco agli altri, per ottenere un rettangolo di 60 × 8, poi riprodurli sette volte e occupare un rettangolo di 56 × 60. (figura 1)*. Si sistemano così 140 scatole e resta uno spazio libero di 4 × 60, nel quale si possono ancora sistemare 7 scatole (dopo rotazione di un quarto di giro) (figura 2)*. Lo spazio libero è allora costituito da una striscia di 1 × 56 e da un quadrato di 4 × 4, cioè 72 cm2 del fondo.
- Il resto di 72 cm2 inutilizzabile, corrispondente alla superficie di 3 rettangoli di 8 × 3, o a 3 scatole, deve incitare alla ricerca di una migliore disposizione e a chiedersi se non si possa eliminare la striscia di 1 × 56.
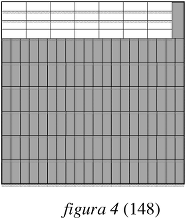
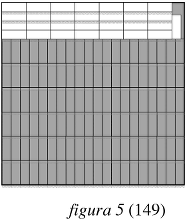
- Una soluzione consiste nel sistemare solo 6 file di 20 rettangoli (figura 3)* per occupare un rettangolo di 48 × 60 (al posto di 56 × 60) con un rettangolo di 12 × 60 (12 è un multiplo di 3) ancora a disposizione, nel quale si possono mettere 7 blocchi di 4 rettangoli (dopo rotazione di un quarto di giro) gli uni di fianco agli altri (figura 4)*. Si sono così sistemati 6 × 20 + 7 × 4 = 148 rettangoli. Non ci sono più strisce vuote e resta a disposizione un rettangolo di 4 × 12 nel quale si può ancora mettere una 149a scatola, con una parte vuota di 24 cm2 del fondo, ma costituita da una striscia di 1 × 12 e da un rettangolo di 3 × 4 nel quale non si può sistemare una 150a scatola. (figura 5)*
- Rimane solo da convincersi che non esistono disposizioni migliori, ma non si dispone di una dimostrazione.



Punteggi attribuiti su 2868 elaborati di 21 sezioni
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 6 | 649 (63%) | 360 (35%) | 19 (2%) | 2 (0%) | 2 (0%) | 1032 | 0.4 |
| Cat 7 | 364 (40%) | 512 (56%) | 31 (3%) | 4 (0%) | 1 (0%) | 912 | 0.65 |
| Cat 8 | 171 (27%) | 398 (62%) | 63 (10%) | 3 (0%) | 2 (0%) | 637 | 0.85 |
| Cat 9 | 21 (14%) | 117 (77%) | 11 (7%) | 0 (0%) | 2 (1%) | 151 | 0.97 |
| Cat 10 | 28 (21%) | 86 (63%) | 19 (14%) | 1 (1%) | 2 (1%) | 136 | 0.99 |
| Totale | 1233 (43%) | 1473 (51%) | 143 (5%) | 10 (0%) | 9 (0%) | 2868 | 0.64 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
Confrontando i dati della tabella sopra si nota subito che il problema è risultato difficile per tutte le categorie a cui è stato proposto. Se poi prendiamo in considerazione il valore medio e le categorie vediamo come passando dalla categoria 6 alla 10 c'è un incremento nei valori ottenuti, ma non così significativi; infatti si passa da 0,4 a 0,8 per la secondaria di primo grado per arrivare a 1 nella secondaria superiore. Comunque se analizziamo invece gli insuccessi, intendendo i punteggi 0 e 1, vediamo come per categoria 6 si raggiunge il 98%, per categoria 7 il 96% e per categoria 8 l'89%, valori sempre troppo alti. Non va meglio nemmeno osservando le due categorie superiori, infatti categoria 9 totalizza il 91% e categoria 10 l'84%.
Non sappiamo con certezza quali siano i tipi di ostacoli che hanno permesso a solo 19 classi su circa 2900 di trovare la risposta esatta (149 e 148 scatole).
La risposta 147 è stata trovata solo dal 5% delle classi, mentre la metà delle classi ha trovato 150 o 140.
Tra quelli che hanno preso 0 punti:
- il 10% non risponde e consegna il foglio in bianco, maggiori sono quelli di categorie inferiori; -il 33% lavora sulle aree e non sui volumi, confondendo i due concetti, infatti spesso calcolano il volume e lo chiamano area, oppure calcolano l'area dello scatolone e della scatola senza affermare che una dimensione è uguale per entrambe, quindi...........e poi lo divide;
- il 20% utilizza i numeri delle misure per combinarli ed operare su essi a caso; - altro 20% utilizza il disegno in 3 dimensioni dello scatolone e della scatola e prova a vedere quante volte potrebbe essere contenuto senza trovare però una strategia adeguata;
- il 17% lavora sulle lunghezze delle dimensioni, le somma , le divide, quelle dello scatolone per quelle della scatola.
Tra quelli che hanno preso 1 punto:
- il 29% trova la soluzione 140; di questi il 38% presenta una soluzione con solo calcoli, mentre il 62% accompagna la soluzione con disegni in 3 D e calcola le file e le colonne;
- il 71% trova la soluzione 150 e tra questi l'84% calcola i due volumi e fa la divisione, mentre il 16% calcola sempre i volumi, ma li chiama aree, confondendo le due e le tre dimensioni.
Tra quelli che hanno preso 2 punti, soluzione 147:
- il 77% presenta la soluzione con calcoli e disegno, lavorando su due dimensioni con disposizione orizzontale e verticale;
- il 23% presenta la soluzione solo con dei disegni adeguati con disposizione orizzontale e verticale.
Quelli che hanno preso 3 o 4 punti non sono presenti nelle categorie da 6 a 8, e anche nelle categorie 9 e 10 rappresentano solo 1%, quindi non vengono qui prese in considerazione.
Più di metà delle classi, a seconda delle categorie, non ha tenuto conto della disposizione delle scatole ed ha effettuato una sola operazione algoritmica: il calcolo del quoziente dei due volumi (60x60x5):(8x3x5)=150. L'ostacolo più rilevante è la scarsa abitudine a trovare altre soluzioni oltre alla prima venuta in mente, infatti non hanno controllato la soluzione finale altrimenti si sarebbero accorti dell'enorme spazio rimasto ancora a disposizione. Alcuni degli insuccessi è dovuto alla sistemazione di 20 scatole di lato 3 sul lato da 60 dello scatolone. Sull'altro lato da 60 né mettono 7 considerando il lato di 8 cm. Alla fine concludono facendo 7x8= 56 non accorgendosi dello spazio vuoto che rimane libero.
Il 29% si è accontentato di una pavimentazione di 20x7 senza rendersi conto che la parte vuota rimasta avrebbe permesso di sistemare ancora 7 scatole.
Dal punto di vista epistemologico o dal punto di vista dello sviluppo delle capacità di visualizzazione nello spazio si può ipotizzare che gli allievi non siano ancora capaci di disporre mentalmente le scatole e che essi abbiano assolutamente bisogno di manipolare le scatole e questo è confermato anche dal fatto che la percentuale di “incomprensione del problema” è bassa passando dalla categoria 6 alla 8. Si può pensare anche che gli ostacoli possano essere di ordine didattico, dato che i volumi vengono trattati solo nella categoria 8. Se gli allievi in classe hanno visto solo delle applicazioni delle formule del volume di un parallelepipedo rettangolo o degli esercizi senza mai risolvere “dei veri problemi”, allora è verosimile che essi utilizzeranno la moltiplicazione o la divisione che hanno sempre usato in questo tipo di attività senza dare senso al loro compito. Allora diventa normale che circa la metà dei gruppi dia la risposta 150 come risultato della divisione dei due volumi.
Tutte queste riflessioni mostrano l'interesse di riprendere in classe il problema proponendo del materiale e dei disegni preparatori di riempimento di scatole e per mostrare che il rapporto dei volumi, 150, è un limite superiore a cui ci si può avvicinare dopo numerose prove tenendo però conto dei limiti fisici legati agli oggetti.
I risultati ottenuti da questo problema ricordano da vicino quelli ottenuti dal problema “La scatola di cubi”; era un problema per categoria 6 e 7, aveva ottenuto punteggi medi di 0,6-0,8 e trattava lo stesso argomento, riempimento di un parallelepipedo rettangolo con cubi di spigolo diverso. Se poi andiamo a confrontare il capitolo “errori” ci accorgiamo che ci troviamo di fronte alle stesse mancanze: scambiano i concetti di area e volume, anche con un linguaggio non adeguato, quindi mostrano difficoltà nel passaggio dalle due alle tre dimensioni e viceversa, privilegiano quasi sempre le soluzioni aritmetiche anche di fronte a dati evidentemente contrari.
Potrebbe essere utile costruire con del cartoncino le scatole e lo scatolone, ignorando di fatto il dato dello spessore.
(c) ARMT, 2015-2024