Une boîte particulière

Identification

Rallye: 25.II.13 ; catégories: 7, 8, 9, 10 ; domaine: 3D
Familles:

• VS - Visualiser dans l'espace
• VS/SV - Traiter des développements de solides

Envoyer une remarque ou une suggestion

Résumé

Reconnaître à partir du dessin de 4 de ses faces rectangulaires, qu’un solide est un prisme droit. Dessiner ses deux autres faces sachant qu’elles ont un seul axe de symétrie.

Enoncé

Tâche de résolution et savoirs mobilisés

- Comprendre qu’il faut commencer en analysant les informations données par les mesures des quatre rectangles.

- Comprendre qu’à partir des quatre faces rectangulaires données, on peut construire un prisme droit.

- Comprendre que les faces données sont des faces latérales et que les deux faces à dessiner sont les deux bases identiques non rectangulaires.

- Remarquer que sur les quatre rectangles, deux ont des mesures totalement identiques et que les quatre rectangles ont une mesure commune.

- Faire des essais de positionnement des faces les unes par rapport aux autres : Essayer de mettre dans des plans parallèles les deux rectangles de mêmes dimensions et constater que les deux faces déjà dessinées ne s’adaptent pas à cette disposition. En déduire qu’ainsi on ne peut pas construire le solide recherché.

- Comprendre qu’il est possible de positionner les faces données les unes au bout des autres en utilisant leur mesure commune et comprendre en refermant la construction que les faces manquantes seront les bases d’un prisme droit.

- Réorganiser le positionnement des faces données pour que les faces manquantes aient un axe de symétrie

- Reconnaître que les bases seront donc des trapèzes isocèles dont les dimensions se déduisent des dimensions des rectangles déjà donnés

- Construire les figures en respectant les mesures

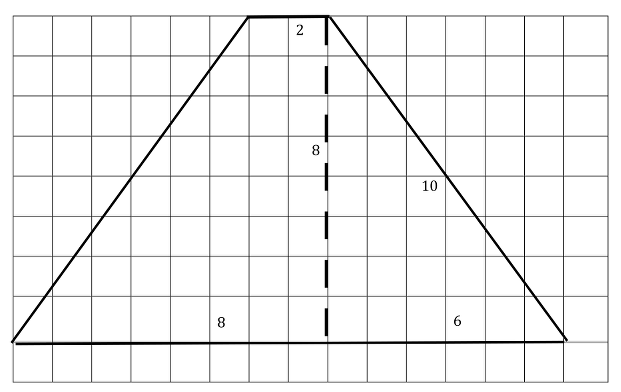
- En construisant un triangle rectangle à l’intérieur du trapèze, on vérifie avec la relation de Pythagore 6, 8, 10 que la hauteur du trapèze sera de 8 côtés de carreaux, le côté oblique de 10 et que la grande base du trapèze mesure 6 + 2 + 6

L’analyse a priori de la tâche de l’élève ci-dessus a été rédigée lors de l’élaboration du problème avant l’épreuve du rallye. Elle est donc encore hypothétique. Elle sera validée, adaptée ou modifiée selon les résultats de l’expérimentation, à la lecture des copies rendues et deviendra l’analyse a posteriori du problème. C’est cette dernière qui permettra de rédiger les rubriques Tâche de résolution et savoirs mobilisées, Procédures, obstacles et erreurs relevées et Indications didactiques de la fiche du problème dans la Banque de problèmes du RMT.

Notions mathématiques

prisme, développement, patron, face, rectangle, trapèze, isocèle, mesure, Pythagore, longueur, angle droit

Résultats

25.II.13

Points attribués, sur 2199 classes de 19 sections:

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Dessin correct des deux figures manquantes ou d’une seule en indiquant que l’autre est identique (un trapèze isocèle avec les côtés mesurant 10-2-10-14 en côtés de carreaux), avec des explications claires
• 3 points: Dessin de deux trapèzes isocèles, mais avec une mesure erronée des côtés obliques
  ou un seul trapèze isocèle correctement dessiné sans préciser que l'autre figure manquante lui est égale
• 2 points: Dessin d’un trapèze isocèle avec toutes les mesures erronées, mais avec des explications
  ou dessin d’un quadrilatère irrégulier qui respecte les mesures des côtés (4, 10, 10 et 14) mais qui ne respecte pas la condition d'avoir un axe de symétrie
• 1 point: Début de raisonnement correct avec une construction d’un quadrilatère qui vérifie deux des mesures
  ou déclaration verbale qui traite d'un trapèze isocèle
• 0 point: Incompréhension du problème

Procédures, obstacles et erreurs relevés

Dans le tableau ci-dessus, on constate qu'environ 60 % des copies ont obtenu 0 ou 1 point et que les meilleurs résultats ont été obtenus par les catégories 9 et 10. Cette tendance dénote une meilleure compréhension du texte, probablement due à un développement cognitif croissant.

Parmi les réponses correctes on ne trouve souvent que le dessin du trapèze isocèle sans explication de la procédure de résolution. La plupart des groupes procèdent par tâtonnement en construisant, avec les faces données, la surface latérale du solide sans avoir une vision mentale de la boîte à construire.

En catégorie 7, la contrainte d'un seul axe de symétrie est rarement prise en compte alors que dans les catégories supérieures, les stratégies adoptées par les élèves semblent correspondre à celles de l'analyse a priori malgré l'utilisation d'un langage approximatif.

L'appropriation du problème s'est révélée difficile vu que le solide proposé, un prisme à base trapézoïdale, est non standard.

De nombreux exemples illustrent les obstacles que rencontrent les élèves à imaginer ce solide particulier dans l'article en bibliographie publié dans la Gazette de Transalpie no 13.

Exploitations didactiques

Le problème peut être utilisé dans des parcours de géométrie solide, avec les objectifs suivants :

- Essayer d’améliorer la visualisation spatiale, une compétence qui ne s'enseigne pas au sens strict de la transmission d'un enseignant à un apprenant, ni par des exercices, ni par des conseils, ni par des impositions. C'est à l'élève de construire cette compétence. Il le fait dès l'enfance en manipulant les objets mis à sa disposition. On croit qu'il « joue », en réalité son activité va bien au-delà de l'aspect ludique : il déplace ces objets, les juxtapose, les empile, les palpe, ...

- Essayer de fournir des images de prismes non standards

- Travailler sur les axes de symétrie des figures planes

Pour plus de détails, voir article en bibliographie.

Pour aller plus loin

Il est essentiel de pratiquer la visualisation spatiale, un aspect qu'il est aujourd'hui plus que jamais essentiel de construire à travers de multiples expériences ciblées de la vie réelle : « observer » un objet les yeux fermés et le décrire dans un langage naturel qui ne devient spécifique qu'à ce moment-là.

Parmi les problèmes du domaine 3D de la banque RMT, certains permettent de reprendre des opérations dans un contexte de boîte, notamment La boîte de sucres (ral. 05.I.03) et Gourmandises (ral. 21.I.01). D'autres sont plus axés sur la visualisation spatiale des faces d'un parallélépipède, comme La boîte à recouvrir (ral. 18.I.04), Boîtes (ral. 17.I.05), Les boîtes de Catherine (ral. 26.F.07), ou les prismes à base triangulaire comme La tente canadienne (ral. 26-I-06).

Bibliographie

Gruppo Geometria 3D / Groupe de Géométrie 3D. C. Bertaccini, A. Canestro, C. Cateni, L. Fazzino, A. Loseto, F. Ricci, R.Santori 2019. UNA SCATOLA PARTICOLARE / UNE BOÎTE PARTICULIÈRE In Gazette de Transalpie no 13. PP 69-87