Le scatole di Caterina

Identificazione

Rally: 26.F.07 ; categorie: 4, 5, 6 ; ambiti: 3D, OPN
Famiglie:

• LAV - Gestire lunghezze, superfici, volumi
• VS - Visualizzare nello spazio
• VS/OA - Contare oggetti nello spazio

Remarque et suggestion

Sunto

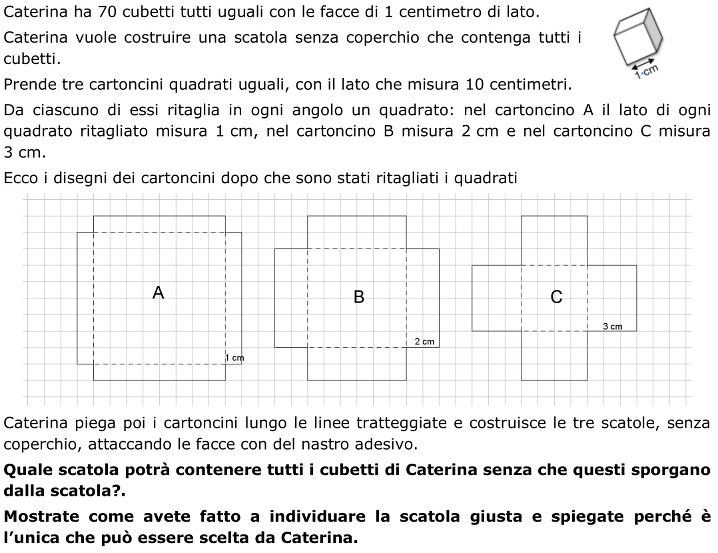
Osservare tre sviluppi di parallelepipedi mancanti di una faccia e stabilire quali di essi può dare origine ad una scatola che possa contenere 70 cubetti tutti uguali.

Enunciato

Compito per la risoluzione e saperi mobilizzati

Analisi a priori

- Osservare le figure e rendersi conto che esse mostrano i tre cartoncini dopo che da ciascuno sono stati ritagliati negli angoli quattro quadrati uguali, ma con lato diverso in ogni cartoncino (1 cm, 2 cm, 3 cm)

- Rendersi conto che, piegando i cartoncini lungo le linee tratteggiate e unendo poi le facce laterali, si ottengono scatole a forma di parallelepipedo a base quadrata con altezze diverse e diverso spigolo di base

- Capire che l’altezza di ogni scatola è uguale al lato di un quadratino ritagliato dal cartoncino e su ogni livello (strato) si può disporre al massimo lo stesso numero di cubetti.

- Capire che per poter riempire le scatole con il maggior numero di cubetti bisogna sistemarli uno vicino all’altro per non lasciare spazi vuoti tra di loro.

- Capire che ogni quadretto che forma la base di ogni scatola coincide con una faccia del cubetto e che perciò sul fondo di ciascuna scatola si potranno sistemare tanti cubetti quanti sono i quadretti

- Contare o calcolare il numero di cubetti che si possono mettere sul fondo di ogni scatola, rispettivamente di 64, 36 e 16 cubetti.

- Poiché l’altezza della scatola A è uguale allo spigolo del cubetto, la scatola si può riempire con un unico strato (64 cubetti, 8×8), mentre la scatola B può contenere due strati di cubetti, quindi la scatola B può contenere al massimo 72 cubetti (36+36 oppure 36×2), la scatola C può contenere tre strati, quindi 48 cubetti (16+16+16 oppure 16×3).

- Concludere che l’unica scatola che può contenere tutti i 70 cubetti è la scatola B.

Oppure:

- Ritagliare le figure e costruire le scatole unendo con il nastro adesivo le facce laterali; se si hanno a disposizione cubetti di 1 cm³ provare a riempire almeno il primo strato per capire come contare tutti i cubetti che ogni scatola può contenere, altrimenti immaginarsi la disposizione dei cubetti. Calcolare poi quanti sono i cubetti che ciascuna scatola può contenere.

Nozioni matematiche

nombre naturel, multiplication, somme, cube, parallélépipède, volume, développement, patron, rectangle, carré

Risultati

26.F.07

Punti attribuiti, su 164 classi di 19 sezioni:

Secondo i criteri determinati nell’analisi a priori:

• 4 punti: Risposta corretta (scatola B) con descrizione chiara e completa (almeno la determinazione del numero massimo di cubetti che ogni scatola può contenere: B 72, A 64, C 48 e i motivi per cui la scatola B è l'unica che può contenere tutti i cubetti perché 72 > 70 mentre 64 e 48 sono minori di 70
• 3 punti: Risposta corretta con descrizioni parziali o poco chiare della procedura (ad esempio determinazione di 72, 64 e 48, senza spiegare la scelta della scatola B)
• 2 punti: Risposta corretta (scatola B) senza descrizione della procedura
  oppure calcolo dei cubetti di ogni scatola (72, 64 e 48), senza dire qual è la scatola scelta.
• 1 punto: Inizio di ricerca coerente per esempio trovato il numero di cubetti che si possono sistemare sulla base di ciascuna scatola (64, 36, 16)
  oppure risposta corretta in base all’affermazione che la scatola A è troppo bassa e che la scatola C è troppo stretta senza tener conto delle altre dimensioni.
• 0 punto: Incomprensione del problema

(c) ARMT, 2018-2025