
Banca di problemi del RMT
3d80-it
 |
Banca di problemi del RMT3d80-it |
|
Envoyer une remarque ou une suggestion
Trovare quanti parallelepipedi rettangolari 1 x 2 x 3 possono essere posizionati in un cubo 8 x 8 x 8.
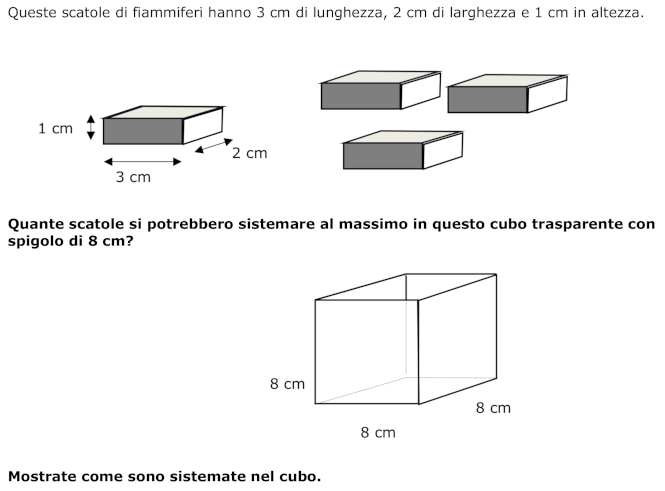
Immaginare le disposizioni differenti delle scatole nel cubo. Considerare il quadrato alla base del cubo e i rettangoli di 2 x 3 che rappresentano le scatole poste “orizzontalmente”. Ad esempio, possiamo disporre 10 rettangoli di 2 x 3 in diverse disposizioni che, ogni volta, rappresentano uno strato di 10 scatole di 1 cm di altezza. Sovrapponendo 8 strati occupiamo l'intero cubo ad eccezione di un “buco” di 4 cm$^2$ o due “buchi” di 2 cm$^2$ nei quali possiamo introdurre prima due scatole poste verticalmente (di base 1 x 2 e di altezza 3) poi una seconda volta.
I saperi necessari sono le proprietà del parallelepipedo rettangolare e del cubo: sei facce, rettangoli o quadrati, otto vertici, il parallelismo di bordi e facce, dritte e piani perpendicolari, l'uguaglianza (isometria) di spigoli e facce, ecc. Tutta questa conoscenza si trova a livello degli oggetti fisici e delle loro osservazioni e manipolazioni; devono ancora essere "matematizzati", a livello di figure geometriche.
parallelepipedo rettangolo, cubo, faccia, rettangolo, quadrato, visione spaziale
Les réponses à la question sur le nombre maximum de boîtes dans le cube sont, pour les 9 classes de la finale internationale 2024 (A trequanda, en Toscane) : 160, 128, 102, 85; 84; 82; 64; 12 et une "non réponse".
Il n’y a pas de feuille blanche, toutes les copies présentent des essais de représentation (voir rubrique suivante).
Si sapeva che la rappresentazione delle scatole del cubo mediante un disegno su un foglio, in due dimensioni, richiede una figura prospettica che non può permetterci di contarle una per una perché non si "vedono" tutte le scatole.
Sette esempi delle nove elaborati:

In questo primo esempio, gli allievi hanno lavorato per strati, che chiamano "soluzione". Accanto alla figura che hanno disegnato (dieci rettangoli 2 x 3 numerati da 1 a 10, in un quadrato 8 x 8 in dimensione reale (cm) e due rettangoli 1 x 2) Quindi in ogni soluzione ci sono al massimo 10 scatole. Abbiamo fatto 10 x 8 in altezza = 80 + 4 cioè le scatole che si possono incastrare in verticale. Risposta. Il numero massimo di scatole che possono trovarsi in un cubo con uno spigolo di 8 cm è 84.

Gli esempi 2 e 3 sono procedure "a strati". Le scatole verticali nell'esempio 2 sono indicate dalle frecce, il numero 85 è molto vicino alla soluzione ottimale, probabilmente c'è un'imprecisione nel conteggio delle scatole verticali. Nell'esempio 3, la piastrellatura della base è composta da 2 x 2 quadrati invece di 2 x 3 rettangoli e risulta nella risposta coerente 128.
L'esempio 4 è una, notevole, rappresentazione in prospettiva con due strati di scatole verticali (64 = 2 x (8 x 4) e difficoltà nel disegnare il terzo strato di scatole poste "dal lato 1 x 2": 18 invece di 20.
L'esempio 5 è una rappresentazione in prospettica con gli spigoli disegnati con un righello, ma rispettando solo una delle tre dimensioni del cubo (altezza 8 cm).
Anche l'esempio 6 è una rappresentazione in prospettica, incompleta e che non consente di individuare il numero di riquadri.
L'esempio 7 cubo aperto ovviamente non permette di arrivare al numero di scatole ricercato.
L'ostacolo principale è la rappresentazione della disposizione delle scatole in 3D su uno schema 2D. Poi, per chi ha pensato ad un disegno delle scatole poste orizzontalmente sul fondo del cubo, un'altra difficoltà è disporre 10 rettangoli di 2 x 3 nel quadrato di 8 x 8.
Solo una classe ha superato queste difficoltà, altre tre hanno disegnato le scatole in basso, con un controllo insufficiente.
Gli altri hanno provato a rappresentare le pile, da diversi punti di vista ma con errori su una delle dimensioni o senza poter effettuare un conteggio preciso dato il numero di scatole invisibili.
Da notare però che non esiste alcun foglio bianco e che tutte gli elaborati presentano tentativi di rappresentazione, in particolare degli 8 piani.
In totale si hanno (8 x 10) + (2 x 2) = 84 scatole. (Ci si può aspettare la risposta «85 scatole» a seguito della divisione di 83 = 512 per 6 il cui quoziente intero è 85 e lil resto 2 (senza tener conto dei vincoli materiali). Si veda La scatola di cubi (ral. 16.II.12 cat 6-10.
La varietà di risposte e rappresentazioni ottenute da 9 classi mostra l'importanza di praticare l'attività Scatole di fiammiferi per avvicinarsi al campo della "geometria spaziale" in classe. Gli esempi sopra riportati sono sufficienti per convincersene. C'è molto lavoro da fare per arrivare a rappresentazioni di oggetti spaziali (3D) su un foglio (2D).
Nelle fasi di discussione e istituzionalizzazione è necessario osservare o sottolineare che le rappresentazioni bidimensionali, per quanto precise possano essere, non consentono di contare con certezza le scatole, per ragioni di opacità, ma che è necessario ricorrere anche a ragionamenti basati su rappresentazioni bidimensionali. In particolare sulle pavimentazione.
Per quanto riguarda le pavimentazione, gli allievi (vedi esempio 1) osservano attraverso esperimenti che i rettangoli 2 x 3 non possono coprire completamente una faccia quadrata 8 x 8. Come possono esserne convinti? Passando "all'aritmetica delle misurazioni" delle area: dividendo 64 (= 8 x 8) per 6 (= 2 x 3) si ottiene un quoziente intero (10) e un resto di 4! È ancora necessario verificare con l'altra disposizione delle scatole sul fondo (vedi esempio 4, dove i primi due strati non hanno spazio vuoto ma rimangono 8 cm$^2$ non occupati nel terzo strato.)
Applicando l'algoritmo di divisione senza tenere conto dei vincoli del cubo e della disposizione delle scatole, arriveremmo a “85 scatole” perché il quoziente di 512 (8 x 8 x 8) per 6 dà un quoziente intero di 85 e un resto di 2. (Tipo di procedura osservato della in più di 50% dei protocolli tra gli allievi delle categorie da 8 a 10, e ben oltre, nel problema La scatola dei cubi (ral. 16.II.12 cat 6-10).
In pratica, l'attività può essere proposta dopo un primo dibattito collettivo in cui gli allievi si scambiano alcune idee per appropriarsi della situazione e delle caratteristiche degli oggetti: le scatole, le loro dimensioni, le loro facce che sono rettangoli; il cubo e le sue dimensioni, il cui “fondo” è un quadrato di dimensioni note, come le sue altre facce che potrebbero diventare il “fondo” se lo posizionassimo su una delle sue “facce laterali”.
La ricerca della soluzione potrebbe poi essere sviluppata in gruppi, con ovviamente la costruzione delle scatole da parte degli studenti, che è il modo migliore per rafforzare le loro conoscenze sul parallelepipedo rettangolare e sul cubo: i diversi sviluppi (pattern), la precisione delle linee, il taglio e la piegatura, ecc.
Per ragioni pratiche è meglio "allargare" le scatole scegliendo unità di lunghezza di 2 cm anziché di 1 cm. Gli oggetti sono più realistici e le manipolazioni sono più facili per i collage. Se ogni allievo della classe ne costruisce due, questo sarà sufficiente per un primo strato.
Jaquet F. (2024) Analyses de la finale internationale de 2024. In Gazette de Transalpie / Gazzetta del Trasalpino 15. pp.77-128