
Banca di problemi del RMT
3d82-it
 |
Banca di problemi del RMT3d82-it |
|
Envoyer une remarque ou une suggestion
Determinare i numeri minimo e massimo di cubi sovrapposti per formare una costruzione su un quadrato di base 3 × 3, della quale è data l’ombra su una parete.
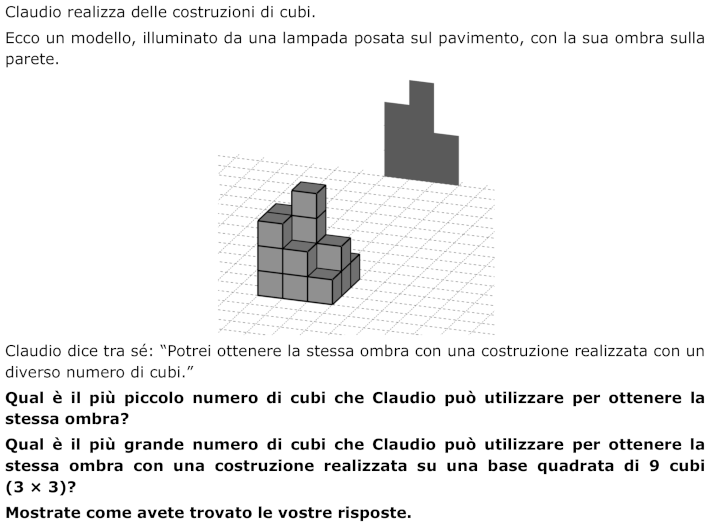
- Percepire l'oggetto, la costruzione nel nostro spazio tridimensionale e la sua ombra, in due dimensioni, e rendersi conto che quest’ombra può essere ottenuta da diverse sovrapposizioni di cubi costruiti su una base di 3 × 3.
- Osservare l'ombra e scomporla in tre rettangoli verticali, da sinistra a destra, essendo il primo l'ombra di una sovrapposizione di 3 cubi, il secondo l’ombra della sovrapposizione di 4 cubi e il terzo di quella di 2 cubi.
- Constatare che la costruzione con il minor numero di cubi e stessa ombra è quella che ha solo queste tre torri, senza niente né davanti né dietro, cioè 9 cubi (3 + 4 + 2).
- Scoprire che la costruzione con il massimo numero di cubi e stessa ombra, è quella che si ottiene mettendo le tre torri precedenti in ciascuno dei tre allineamenti disponibili sulla griglia, "davanti", "al centro" e "dietro" ed è quindi composta in totale da 27 cubi 3 × 9.
cubo, faccia, conteggio
Punteggi attribuiti su 2041 classi di 20 sezioni:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 5 | 138 (17%) | 122 (15%) | 224 (28%) | 119 (15%) | 192 (24%) | 795 | 2.13 |
| Cat 6 | 185 (15%) | 206 (17%) | 284 (23%) | 178 (14%) | 393 (32%) | 1246 | 2.31 |
| Totale | 323 (16%) | 328 (16%) | 508 (25%) | 297 (15%) | 585 (29%) | 2041 | 2.24 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
Secondo i criteri dell'analisi a priori :