Le nombre de Charles

Identification

Rallye: 14.II.10 ; catégories: 5, 6, 7 ; domaine: AL
Familles:

• AA - Passer de l'arithmétique à l'algèbre
• AA/TN - Trouver un nombre

Remarque et suggestion

Résumé

Trouver le nombre naturel tel que, en lui appliquant la suite des cinq opération: "ajouter 20", "diviser par 3", "soustraire 2", "multiplier par 4" et "soustraire 10", on aboutit au double de ce nombre.

Enoncé

Tâche de résolution et savoirs mobilisés

A partir d’un nombre naturel, effectuer la suite d’opérations : ajouter 20, diviser par 3, soustraire 2, multiplier par 4 et soustraire 10 pour finir et obtenir le double du nombre de départ. Trouver ce nombre et vérifier l’unicité de la solution.

Travailler par algèbre, désigner le nombre cherché par une lettre, n ; écrire la suite des opérations ; résoudre l’équation correspondante. vérifier qu’elle n’a qu’une solution.

Ou, au niveau arithmétique, travailler par essais successifs, plus ou moins organisés.

Notions mathématiques

addition, soustraction, multiplication, division, calcul littéral

Résultats

14.II.10

Sur 657 copies examinées de sept sections, les points attribués sont les suivants:

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Réponse 13 avec le détail des calculs ou des essais effectués, où l’on perçoit l’unicité de la solution
• 3 points: Réponse 13 avec le détail des calculs ou des essais effectués, mais sans mention de l’unicité
• 2 points: Réponse 13 avec des justifications peu claires ou avec une vérification seulement
  ou procédure correcte mais avec une erreur de calcul ou l’oubli d’une étape
• 1 point: Réponse 13 sans aucune explication ou début de recherche
• 0 point: Incompréhension du problème

Ces résultats sont confirmés par ceux de six autres sections, avec des moyennes respectives de 1,4, 1,5 et 2,0 points pour les catégories 5, 6 et 7.

Procédures, obstacles et erreurs relevés

De l’analyse a posteriori des 314 copies des sections de Parme, Sienne et Puglia, c'est une procédure arithmétique par essais (plus ou moins organisés et explicites), qui a été mise en oeuvre dans la quasi totalité des cas : on part de 1, on suit la séquence des instructions et on vérifie que ça ne va pas, on passe à 2 et on continue ainsi en essayant les nombres suivants jusqu'à 13, qui vérifie la condition requise. Cette procédure permet souvent de se rendre compte qu'on peut éliminer les nombres qui, divisés par 3, donnent des valeurs non entières et que, par conséquent, on peut se limiter à la suite des nombres qui lorsqu'on leur ajoute 20 sont multiples de 3, c'est-à-dire: 1, 4, 7, 10, 13, 16, ...

Dans quelques copies la procédure est un “algorithme de calcul” qui représente sous forme symbolique la séquence + 2 ; : 3 ; – 2 ; × 4 : – 10.

Dans chaque cas, dès que la solution "13" est atteinte, la recherche s'arrête, étant entendu que la solution est unique. La manière dont est posée la question n'induit d'ailleurs pas la recherche d'une autre solution.

L'observation des résultats fait apparaître un nombre très élevé de copies (25%) dans lesquelles apparaissent des écritures incorrectes. En particulier, un usage fréquente du signe “=” comme opérateur unidirectionnel (signifiant “est le résultat de ... " et non comme relation d'équivalence (par exemple: 13 + 20 = 33 : 3 = 11 - 2 = 9 × 4 = 36 - 10 = 26. On néglige ici l'usage des parenthèses pourtant indispensables qui entraîne des amiguïtés dans l'interprétation des écritures symboliques (par exemple si N est la valeur inconnue on obtient l'écriture N + 20 : 3 - 2 × 4 – 10 = 2N). Dans quelques copies de catégorie 5 ou de catégories 6, on note des invertions entre la deuxième consigne (divisez par 3) et de la troisième (soustrayez 2) comme si elles étaient implicitement commutatives.

Ces manières d'écrire les opérations, comme on le sait bien, représentent des obstacles à l'usage du langage algébrique et à la construction du concept d'équation.

Exploitations didactiques

Le problème, proposé en classes de catégories. 5, 6, 7 (mais aussi 8), permet aux élèves, après avoir répété les mêmes opérations plusieurs fois avec des nombres différents, de se rendre compte que ce qui reste constant est l’algorithme, c'est-à-dire la séquence des opérations à effectuer, et qu'on peut trouver un moyen de représenter cette séquence sous une forme symbolique. Penser à indiquer le nombre à trouver avec une lettre ou un autre symbole va permettre d'arriver, assez facilement et spontanément, à écrire une équation.

Les commentaires de certains enseignants qui ont vécu le problème, transversalement, en première, deuxième et troisième années du collège se résument ainsi :

//Le problème apparaît intéressant pour l'enseignement parce que ://

1) il se situe dans un contexte qui attire l'attention par sa similitude avec de nombreux jeux qui circulent entre les enfants et leur paraît donc plaisant ;

2) le texte, simple et schématique, favorise l'appropriation de la tâche ;

3) il fournit des procédures de résolution à la fois arithmétiques et algébriques ;

4) il se prête à la construction d'expressions ou d'équations ;

5) il offre la possibilité d'une vérification indépendante, sans l'intervention de l'enseignant.

Le problème pourrait être proposé (ou re-proposé) dans des classes de catégories 8 ou 9, pour ouvrir la voie à la manipulation de l'écriture symbolique en la simplifiant, sans en altérer la « validité » (principes d'équivalence), afin d'arriver à la détermination de l'inconnue, abordant ainsi l'étude des équations en tant que "objets mathématiques".

Il peut donc aussi permettre la comparaison entre la méthode algébrique et des procédures arithmétiques par essais, qui impliquent, pour chaque valeur considérée, l'exécution répétitive d'une certaine séquence de calculs. Cependant, il faut noter que certains enseignants pensent que "pour un début d'équations ce problème produit une équation trop complexe".

Enfin, on observe qu'en modifiant les variables didactiques (par exemple, le domaine numérique du nombre initial, la séquence et la nature des opérations, les informations sur ce qu'il faut obtenir), l'enseignant, ou les élèves eux-mêmes, peuvent produire des variantes du problème et donc différents types d'équations, avec l'opportunité d'approfondir les réflexions et les discussions en classe.

Pour aller plus loin

Dans la copie suivante, de catégorie 6, la "procédure algorithmique" est bien résumée au moyen d'un tableau indiquant les valeurs initiales et celles obtenues progressivement, et dans lequel la nécessité de ne considérer que les nombres de la suite 1, 4, 7, ...

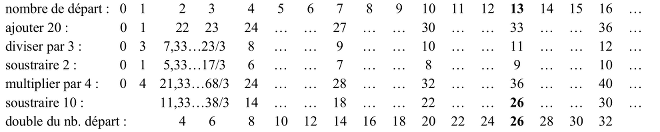
Dans ce tableau, nous notons qu'au fur et à mesure que les nombres 1, 4, 7, 10,… augmentent de 3 par 3. les nombres finaux obtenus avec la procédure algorithmique, c'est-à-dire 10, 14, 18, 22,…, augmentent de 4 en 4.

Une telle observation est bien soulignée aussi dans une copie de catégorie. 5 et aussi dans l'une de catégorie 7 : En partant du nombre 1, nous n'avons considéré que les nombres divisibles par 3 et le seul qui a doublé était le nombre 13. Puis nous avons découvert que le rythme des nombres initiaux est toujours +3, tandis que celui des nombres finaux est toujours + 4 .

Ces observations pourraient conduire à affirmer l'unicité de la solution, ce dont les élèves n'ont cependant pas ressenti la nécessité.

Dans certaines copies de catégories 7 (9 sur 109 analysées) le langage algébrique est utilisé : le nombre à rechercher est indiqué par une lettre (N ou x) et les conditions du texte sont traduites par une écriture algébrique, qui est en fait une équation dont on trouve la solution en remplaçant, de temps en temps, l'inconnue par un nombre naturel jusqu'à ce qu'on arrive à la vérification de l'égalité.

En particulier, dans une copie on lit : Nous avons d'abord essayé de « résumer » les différentes opérations dans une formule [(x + 20) : 3 - 2] × 4 - 10 = 2x. Les élèves montrent qu'ils maîtrisent le concept de résolution d'une équation "en acte", puisqu'ils continuent en substituant à x des nombres qui "ajoutés à 20 sont divisibles par 3" jusqu'à ce qu'ils trouvent 13, ce qui rend l'écriture vraie. Dans deux autres cas, seul le premier terme de l'équation apparaît et est utilisé comme « expression fonctionnelle ».

Il convient également de mentionner une dernière copie dans laquelle l'équation x = [(2x + 10) : 4 + 2] × 3 - 20 est posée et résolue correctement, appelée par les étudiants « inverse » puisqu'elle s'obtient de manière originale, en procédant à rebours dans la reconstruction des relations entre les données.

Bibliographie

Doretti, L., Medici, D., Rinaldi, M. G., Salomone, L.: 2007, ‘Costruzione del concetto di equazione: dalla messa in formula alla risoluzione di equazioni e sistemi lineari’, in L. Grugnetti, F. Jaquet, D. Medici, M.G. Rinaldi (Eds.) I problemi come supporto per l’apprendimento: il ruolo del RMT, Vol. 6, Dipartimento di Matematica dell’Università di Parma, Sezione di Parma dell’ARMT, ARMT [pubblicato anche in L'educazione Matematica, Anno XXVIII, Serie VIII, Vol. 3, n. 3 (2007), 13-30].

Doretti, L., Medici, D., Rinaldi, M. G., Salomone, L.: 2008, ‘Costruzione del concetto di equazione: un possibile percorso con i problemi del RMT’, in L. Grugnetti, F. Jaquet, G. Bellò, R. Fassy, G. Telatin (Eds.) RMT fra pratica e ricerca in didattica della matematica, Vol. 7, Centro Risorse per la Didattica della Matematica, Sezione della Valle d’Aosta dell’ARMT, ARMT.

Malara N., Navarra G.: 2003, Quadro teorico di riferimento e glossario – Progetto ArAl, Pitagora Editrice Bologna. Rinaldi M.G., Medici D.: ‘Un approccio costruttivo alla formalizzazione’, in P.Vighi (Eds.) Progettare Lavorare Scoprire, Grafiche Step editrice, Parma, 2010, 107-118, ISBN 88 7898 054 4

(c) ARMT, 2006-2024