Étranges animaux

Identification

Rallye: 26.II.03 ; catégories: 3, 4, 5 ; domaines: OPN, AL
Familles:

• AM - Additionner et multiplier des nombres naturels
• MEQ - Etablir puis résoudre des (in)équations
• MEQ/EQL - Résoudre un système d’équations linéaires

Envoyer une remarque ou une suggestion

Résumé

Connaissant le poids de deux compositions obtenues avec un nombre différent de pièces de deux formes élémentaires, déterminer le poids d'une troisième composition obtenue avec des pièces similaires.

Enoncé

Tâche de résolution et savoirs mobilisés

Analyse a priori

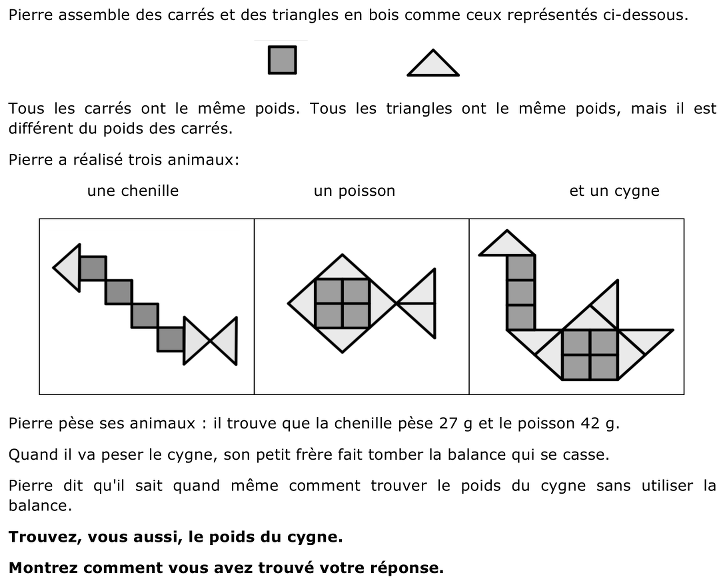
- Observer que pour toutes les compositions, il n’y a que deux types de pièces

- Décrire chaque composition en fonction du nombre et du type de pièces utilisées :

• Chenille : 4 carrés et 3 triangles
• Poisson : 4 carrés et 6 triangles
• Cygne : 7 carrés et 7 triangles

− Procéder par déduction en regardant les différences.

− Comparer le nombre de carrés et de triangles dans la chenille et dans le poisson.

− En déduire que le nombre de carrés est le même et que le poisson est composé de 3 triangles de plus. Comprendre que la différence de poids est due à la présence de trois triangles en plus.

− Déduire que trois triangles pèsent 15 g (42 – 27) ; par conséquent un triangle pèse 5 g (15 : 3).

− Connaissant le poids d’un triangle, trouver celui d’un carré. Par exemple en utilisant la « chenille ». Quatre carrés pèsent 12 g (27 – 15) ; par conséquent un carré pèse 3 g (12 : 4) .

− Calculer le poids du cygne constitué de sept carrés et sept triangles : 56 g (7 × 3 + 7 × 5).

Ou, donner des valeurs aléatoires au poids de chaque pièce, en adaptant les valeurs suivantes.

− Calculer les poids de la chenille et du poisson et s’arrêter lorsque les deux valeurs conviennent.

− Appliquer ces valeurs au calcul du poids du cygne.

Notions mathématiques

nombre naturel, somme, addition, multiplication, équation, égalité, différence, déduction, substitution, division

Résultats

26.II.03

Points attribués, sur 2426 classes de 8 sections:

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Réponse correcte (56 g) avec le détail des calculs et de la procédure suivie
• 3 points: Réponse correcte mais la procédure et les calculs effectués ne sont pas bien décrits,
  ou procédure correcte et bien décrite mais avec une erreur de calcul.
• 2 points: Réponse correcte sans aucune trace de la procédure suivie,
  ou détermination correcte des poids du triangle et du carré, avec les détails des calculs sans le calcul du poids du cygne.
• 1 point: Début de recherche cohérente (par exemple, identifier le nombre de triangles et de carrés dans chaque figure).
• 0 point: Incompréhension du problème (par exemple, attribuer le même poids au carré et au triangle).