
Banca di problemi del RMT
fn13-it
 |
Banca di problemi del RMTfn13-it |
|
Determinare l’area della parte grigia di una decorazione, su carta quadrettata, a partire da una parte del disegno e dal dato dell’area totale della parte bianca.
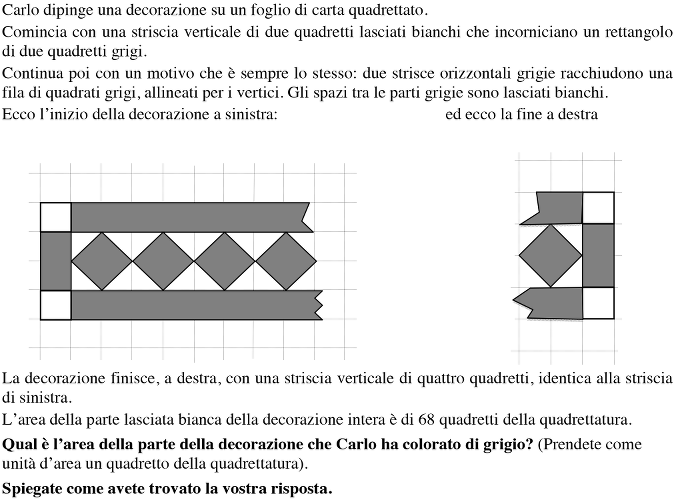
- Osservare il disegno ed eventualmente proseguirlo per capire le regole di costruzione.
- Rendersi conto che si possono calcolare facilmente le aree bianche e grigie delle due colonne di destra e di sinistra, che l’area dei quadretti e dei differenti triangoli bianchi si determina con la scomposizione delle unità della quadrettatura, ma che la lunghezza delle strisce orizzontali o il numero dei quadretti grigi non è conosciuto e impedisce il calcolo diretto delle loro aree.
- Un primo modo di «aggirare l’ostacolo» è quello di continuare il disegno fino ad ottenere i 64 quadretti (per esempio, con i 5 quadrati dei due frammenti disegnati si arriva soltanto a 14 quadretti bianchi interi, con 10 quadrati neri si arriverebbe a 24 quadretti bianchi …) e di fermarsi a 32 quadrati neri e di determinare l’area grigia.
- Una procedura più globale consiste nell’occuparsi della parte tra le due colonne esterne (composte di 4 quadretti bianchi e 4 grigi) per interessarsi soltanto dei 64 quadretti bianchi rimanenti, constatare le ripetizioni di motivi verticali comprendenti un quadrato nero, quattro piccoli triangoli bianchi e due strisce di cui si calcolano facilmente le aree rispettive in unità della quadrettatura: 2 bianchi, 6 (2 + 2+ 2) grigi; dedurne che ci sono 32 motivi ripetuti e calcolare l’area grigia totale, per esempio (32 × 6) + (2 × 2) = 192 + 4 = 196
Oppure: sempre in una procedura globale, constatare l’uguaglianza delle aree grigie e bianche (64 e 64) tra le due strisce orizzontali, ciò che permette di trovare che ci sono 32 quadrati grigi e di determinare la lunghezza delle due strisce orizzontali grigie, poi la loro area per arrivare finalmente a un calcolo del tipo: (2 × 64) + 64 + (2 × 2) = 196
Ci sono ancora numerosi altri modi di organizzare le parti delle figure e i calcoli corrispondenti.
Punteggi attribuiti su 2542 elaborati di 21 sezioni:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 5 | 429 (75%) | 51 (9%) | 37 (6%) | 16 (3%) | 40 (7%) | 573 | 0.58 |
| Cat 6 | 831 (79%) | 105 (10%) | 47 (4%) | 17 (2%) | 46 (4%) | 1046 | 0.41 |
| Cat 7 | 646 (70%) | 64 (7%) | 41 (4%) | 27 (3%) | 145 (16%) | 923 | 0.87 |
| Totale | 1906 (75%) | 220 (9%) | 125 (5%) | 60 (2%) | 231 (9%) | 2542 | 0.62 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
(Commento provvisorio in attesa di analisi a posteriori degli elaborati degli studenti):
Il fallimento quasi totale (tre quarti di "incomprensione del problema" nel complesso) rivela difficoltà troppo elevate per le categorie 5 e 6.
Ci sono molte ambiguità relative a la figura, molti elaborati mostrano il fregio completato tra le due parti, che comprende 8 o 9 quadrati centrali. I quattro quadrati bianchi delle colonne agli estremi non sono sempre stati considerati correttamente nel trovare il numero di ripetizioni tra le estremità.
La conversione dei triangoli bianchi in quadrati di griglia, o dei quadrati grigi del centro del fregio in quadrati di griglia, non è chiara.
Poche copie mostrano una chiara scomposizione dei moduli che si ripetono in verticale.
Groupe fonction (2016). La décoration de Charles. Etude ARMT (http://www.projet-ermitage.org/ARMT/doc/etude-fn13-fr.pdf)
(c) ARMT, 2015-2024