La spirale des cure-dents (II)

Identification

Rallye: 29.II.19 ; catégories: 9, 10 ; domaines: FN, OPN
Familles:

• SF - Etudier des suites de figures
• SN - Traiter une suite numérique

Envoyer une remarque ou une suggestion

Résumé

Trouver le 50e terme d’une suite de nombres 3 ; 8 ; 15 ; 24 ; 35 ; … (à déterminer à partir du dénombrement de cure-dents organisés en spirales successives)

Enoncé

Tâche de résolution et savoirs mobilisés

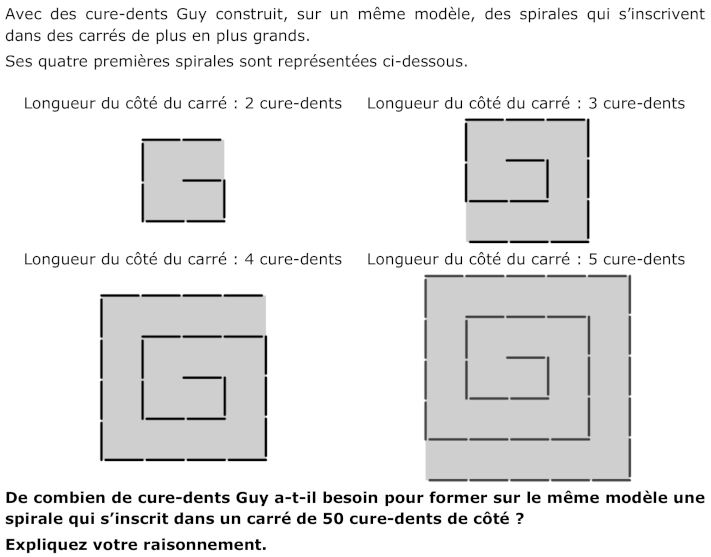
Analyse de la tâche a priori

- Analyser les dessins de spirales pour identifier le modèle sur lequel elles sont constituées en partant du côté du carré (3 segments ayant pour longueur le côté du carré n, 2 segments de longueur (n - 1), 2 segments de longueur (n - 2) , …., 2 segments de longueur 1) ou inversement en partant du centre.

- Faire la somme des cure-dents de chaque spirale et en construire éventuellement quelques autres pour trouver les premiers termes de la suite et les organiser progressivement (voir exemple des deux premières lignes du tableau suivant)

Passer en mode numérique et comprendre la logique qui permet de compléter le tableau sans dessiner les spirales :

- Soit observer qu’on peut passer d’un nombre au suivant en ajoutant les nombres impairs successifs à partir de 7 (3e ligne). Cette méthode exige une cinquantaine d’additions successives.

- Soit en remarquant que le nombre de cure-dents (N) est le produit de deux nombres qui diffèrent de 2 : n et n + 2. Il s’agit de la fonction qui permet de passer directement de la dimension de la spirale au nombre de cure-dents N = n(n + 2.

- Soit en repérant que la suite des carrés de la dimension N de la spirale augmentée de 1 donne la suite des carrés des entiers (n + 1)2 : 9, 16, 25, 36, 49 et en constatant que les nombres de cure-dents valent 1 de moins que ces carrés. Il s’agit aussi d’une fonction qui permet de passer directement de la dimension de la spirale au nombre de cure-dents N = (n + 1)2 - 1

- …

(Les formules (n + 1)² - 1 = n(n + 2) peuvent aussi être obtenue à partir de l’analyse de la spirale de côté n mentionnée précédemment, de la connaissance de la formule qui donne la somme des n - 1 premiers nombres naturels et de connaissances algébriques sur le calcul littéral)

Notions mathématiques

progression, suites, spirale, somme, nombre naturel, fonction, rapports, relations quadratiques

Résultats

29.II.19

Points attribués sur 273 classes de 9 sections:

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Réponse correcte (2600 cure-dents) avec des explications claires présentant le raisonnement suivi pour montrer que la solution trouvée est générale ou trouvée à partir d’une conjecture basée sur l’étude d’au moins 5 spirales
• 3 points: Réponse correcte (2600 cure-dents) avec des explications partielles ou pas suffisamment étayées
• 2 points: Réponse erronée avec identification d’une règle qui permet de calculer les termes de la suite
  ou réponse correcte sans explications
• 1 point: Début cohérent de recherche (par exemple dessin d’une cinquième spirale)
• 0 point: Incompréhension du problème

Procédures, obstacles et erreurs relevés

Procédures

Reconnaissance de la régularité dans la construction des spirales en prenant le côté du carré n x (n + 2) comme variable indépendante.

Reconnaissance de la régularité des quotients entre la longueur de la spirale et le côté du carré (8 : 2 = 4, 15 : 3 = 5, 24 : 4 = 6, ... , ? : 50 = 52), somme de trois fois le côté du carré et deux fois les branches de la spirale intérieure (3 x 50 + 249 + 2 x 48 + … + 2 x 3 + 2 x 2 + 2 x 1 = 2600).

Observation que les branches paires de la spirale peuvent être réarrangées pour obtenir des carrés concentriques de côté pair. Le calcul du nombre total de cure-dents s'obtient donc en multipliant les longueurs de toutes les branches paires de la spirale par 4. (2 + 4 + 6 + 8 + … + 50) x 4 = 2600.

Repérer la régularité dans la somme du périmètre du carré extérieur diminué de 1 avec la longueur de la partie intérieure de la spirale reconnue comme le produit du côté du carré extérieur diminué de 1 [(périmètre du carré) – 1 + longueur de la spirale interne, (périmètre du carré) – 1 + (côté du carré ) – 1)²), L x 4 – 1 + (L – 1)² = 4 x L – 1 + L² - 2 x L + 1 = L² + 2 x L).

Reconnaissance de la relation entre le nombre de cure-dents de la branche extérieure de la spirale, de la branche intérieure de la spirale et le nombre de cure-dents du côté du carré en les considérant comme trois quantités indépendantes. (ni = (ne/4) x (n – 1), avec ni = nombre de cure-dents internes, ne = nombre de cure-dents externes, n = nombre de cure-dents sur le côté du carré). Résolution du problème par essais.

Obstacles et erreurs relevés

Utilisation de la proportion

Erreurs de calcul

Erreur dans la reconnaissance de la régularité (n x (n–2))

Exploitations didactiques

Comparer les différentes stratégies en observant comment la même formule peut être obtenue de différentes façons.

Travailler avec du matériel concret (manipulations) dans les classes des écoles primaires.

Proposer des dessins sur un quadrillage.

Travail en classe sur un tableur.