Le spirali di stuzzicadenti (II)
Identificazione
Rally:
29.II.19 ; categorie:
9, 10 ; ambiti:
FN,
OPNFamiglie:
Envoyer une remarque ou une suggestion
Sunto
Determinare il numero di stuzzicadenti necessari per realizzare una spirale di lato 50 costruita per successione a partire dai primi quattro passi assegnati..
Enunciato
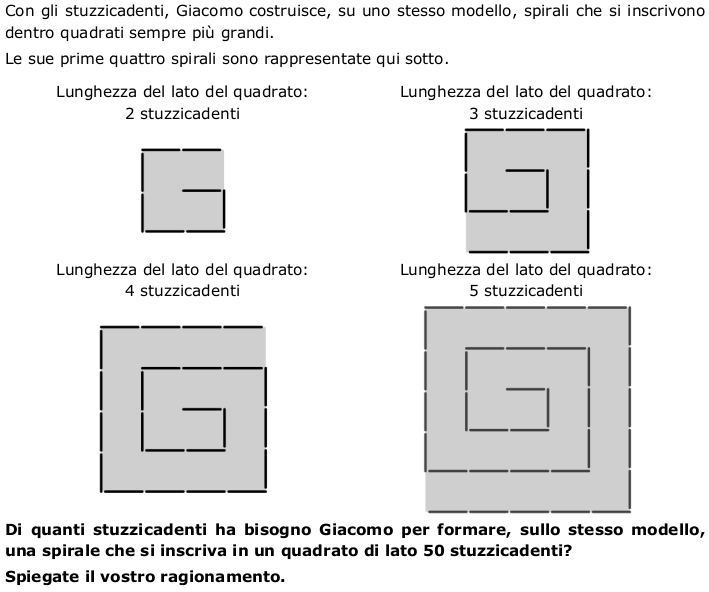
Compito per la risoluzione e saperi mobilizzati
- Analizzare i disegni delle spirali per identificare il modello sul quale sono costruite: sono inserite in quadrati di lato crescente, ogni spirale si ottiene completando la spirale precedente, ($3$ lati per il quadrato $n$, $2$ lati per il quadrato $n − 1$, $2$ lati per il quadrato $n – 2$, ..., $2$ lati per il quadrato $1$) o, inversamente, partendo dal centro.
- Sommare gli stuzzicadenti di ogni spirale dell’immagine, costruirne eventualmente qualcun’altra per trovare i primi termini della successione e organizzarle progressivamente (vedere gli esempi delle due prime righe della tabella seguente):
- Passare alla modalità numerica e comprendere la logica che permette di completare la tabella senza disegnare le spirali:
- sia osservando che si può passare da un numero al successivo aggiungendo i numeri dispari successivi a partire da $7$ ($3$ª riga). Questo metodo prevede una cinquantina di addizioni successive;
- sia accorgendosi che il numero di stuzzicadenti ($N$) è il prodotto di due numeri che hanno differenza $2$ ($n$ e $n + 2$). Questa è la funzione che permette di passare direttamente dalle dimensioni della spirale al numero di stuzzicadenti;
- sia identificando i quadrati dalla dimensione delle spirali aumentate di $1$ ($n – 1$), $9$, $16$, $25$, $36$, $49$ e scoprendo che il numero degli stuzzicadenti vale $1$ in meno di questi quadrati. Questa funzione permette di passare direttamente dalle dimensioni della spirale al numero degli stuzzicadenti $N = (n + 1)^2 – 1$;
- ...
- (Le formule $(n + 1)^2 – 1 = n (n + 2)$ possono essere ottenute a partire dall’analisi della spirale di lato $n$ ricordata precedentemente, dalla conoscenza della formula che permette di trovare la somma dei $n – 1$ primi numeri naturali e dalle conoscenze algebriche sul calcolo letterale).
Nozioni matematiche
progressione, successione, spirale, somma, numero naturale, funzione, scarto, rapporto, relazione quadratica
Risultati
29.II.19
Punti attribuiti su 273 classi di 9 sezioni:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|
| Cat 9 | 23 (17%) | 19 (14%) | 10 (7%) | 20 (15%) | 63 (47%) | 135 | 2.6 |
|---|
| Cat 10 | 26 (19%) | 9 (7%) | 9 (7%) | 13 (9%) | 81 (59%) | 138 | 2.83 |
|---|
| Totale | 49 (18%) | 28 (10%) | 19 (7%) | 33 (12%) | 144 (53%) | 273 | 2.71 |
|---|
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. |
Secondo i criteri determinati nell’analisi a priori:
- 4 punti: Risposta corretta ($2 600$ stuzzicadenti) con spiegazioni chiare che comprovino il ragionamento seguito per mostrare che la soluzione trovata è generale o trovata a partire da una congettura basata sullo studio di almeno $5$ spirali.
- 3 punti: Risposta corretta con spiegazioni parziali o non sufficientemente motivate.
- 2 punti: Risposta errata a causa di un errore di calcolo, ma con identificazione di una regola che permetta di calcolare i termini della successione
oppure risposta corretta senza spiegazioni. - 1 punto: Inizio di ricerca coerente (per esempio il disegno della quinta spirale).
- 0 punto: Incomprensione del problema.
Procedure, ostacoli ed errori rilevati
Procedure
- Riconoscimento della regolarità nella costruzione della spirale considerando come variabile indipendente il lato del quadrato n•(n + 2).
- Riconoscimento della regolarità nei quozienti tra la lunghezza della spirale e il lato del quadrato (8:2 = 4, 15:3 = 5, 24:4 = 6, … , ? : 50 = 52), somma di tre volte il lato del quadrato e due volte i rami della spirale interna (3•50 + 2•49 + 2•48 + … + 2•3 + 2•2 + 2•1 = 2600).
- Osservazione che i rami di spirale di lato pari possono essere ridisposti in modo da ottenere quadrati concentrici di lato pari, in questo modo il calcolo del numero totale di stuzzicadenti si ottiene moltiplicando per 4 le lunghezze di tutti i lati pari della spirale (2 + 4 + 6 + 8 + … + 50)•4 = 2600.
- Individuazione della regolarità nella somma tra il perimetro del quadrato esterno diminuito di 1 e la lunghezza della porzione interna di spirale riconosciuta come prodotto del lato del quadrato esterno diminuito di 1 per se stesso [(perimetro quadrato) - 1 + lunghezza spirale interna, (perimetro quadrato) – 1 + (lato quadrato - 1)2], L•4 –1 + (L – 1)2 = 4•L – 1 + L2 – 2•L + 1 = L2 + 2•L).
- Riconoscimento della relazione tra il numero di stuzzicadenti del ramo esterno della spirale, del ramo interno della spirale e il numero di stuzzicadenti del lato del quadrato considerandole tre grandezze indipendenti (ni = (ne/4)•(n – 1), con ni = numero stuzzicadenti interni, ne = numero stuzzicadenti esterni, n = numero stuzzicadenti lato del quadrato).
- Risoluzione del problema per tentativi.
Ostacoli ed errori rilevati
Uso improprio della proporzionalità
Errori di calcolo
Errore nel riconoscimento della regolarità (n•(n–2))
Indicazioni didattiche
Confrontare le diverse strategie osservando come si possa ottenere la stessa formula in più modi diversi.
Lavorare con materiale concreto (manipolazione) nelle classi di primaria.
Proporre i disegni su uno sfondo quadrettato.
Lavorare in classe su una tabella.



