Di figura in figura

Identificazione

Rally: 30.I.14 ; categorie: 7, 8, 9, 10 ; ambiti: FN, GP
Famiglie:

• SF - Studiare successioni di figure
• SN - Gestire una successione numerica

Envoyer une remarque ou une suggestion

Sunto

Dati i primi tre elementi di una successione di figure regolari, disegnate su carta quadrettata e colorate di bianco e grigio, determinare la posizione di un’altra figura della successione, a partire dalla relazione tra l’area di questa e quella della figura di posto 7.

Enunciato

Compito per la risoluzione e saperi mobilizzati

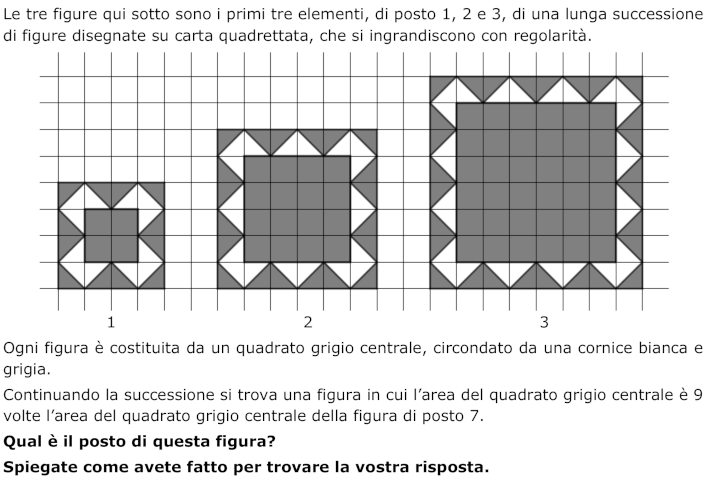
Analisi a priori

- Osservare le figure presenti nel testo e rendersi conto che ci sono caratteristiche che variano ed altre che rimangono costanti. Per esempio, da una figura all’altra, variano: la lunghezza del lato del quadrato interno grigio, la lunghezza del lato del quadrato grande che forma la figura, il numero dei triangoli sia grigi che bianchi della cornice. Ciò che non varia invece è la modalità di decorazione della cornice e il suo spessore (di un lato di quadretto della quadrettatura).

- Rendersi conto che il numero di triangoli grigi, il numero di triangoli bianchi, la lunghezza del lato della figura, la lunghezza del lato del quadrato grigio, la sua area… dipendono dalla variabile n, che indica il posto della figura, e percepire che, fra tutte le grandezze in gioco, la lunghezza del lato del quadrato grigio interno è la più « utile » per orientarsi nella successione.

- Affrontare la fase di risoluzione, a partire dalle osservazioni precedenti, indentificando le regolarità della successione, per esempio mettendo in evidenza il posto n, la lunghezza del lato e l’area del quadrato centrale (espressi in lato e area di un quadretto della quadrettatura):

• la figura di posto 1 ha un quadrato interno di lato 2 e area 4,
• la figura di posto 2 ha un quadrato interno di lato 4 e area 16,
• la figura di posto 3 ha un quadrato interno di lato 6 e area 36,
• ...
• la figura di posto 7 ha un quadrato interno di lato 14 e area (14)$^2$ = 196
• la figura di posto n ha un quadrato interno di lato 2n e area (2n)$^2$.

- la figura cercata di posto incognito, che indichiamo provvisoriamente con X, ha un quadrato interno di lato 2X e un’area di de 196 x 9 = 1764 = (2X)$^2$ per arrivare finalmente a 2X = √1764 = 42 e al posto della figura cercata: X = 21

Nozioni matematiche

successione, idea di funzione

Risultati

30.I.14

Punteggi attribuiti sur 2250 classi di 21 sezioni

Secondo i criteri dell'analisi a priori :

• 4 points: Risposta corretta (posto 21) con spiegazione chiara della procedura seguita (descritte le relazioni individuate tra gli elementi delle figure e come sono state utilizzate)
• 3 points: Risposta corretta con spiegazioni poco chiare o incomplete
• 2 points: Risposta corretta senza spiegazioni,
  oppure oppure qualche errore nel calcolo delle aree per arrivare al posto corretto
• 1 point: Inizio di ricerca coerente (per esempio, determinate correttamente le aree del quadrato grigio della figura 7 e quella del quadrato grigio della figura richiesta, ma non individuata correttamente la sua posizione,
  oppure trovata la relazione tra posizione della figura ed area del suo quadrato grigio,
  oppure disegnata correttamente qualche altra figura della sequenza)
• 0 point: Incompréhension du problème

Procedure, ostacoli ed errori rilevati

Procedure

1) Procedura algoritmica: 7 × 2 = 14 (lato del quadrato interno alla figura di posto 7), 14$^2$ = 196 (area del quadrato interno alla figura di posto 7), 196×9=1764 (area del quadrato interno alla figura cercata), √1764=42 (lato del quadrato interno alla figura cercata), 42:2 = 21 (posto della figura cercata), con alcune varianti, specialmente in cat.7-8, in cui la radice quadrata è stata sostituita dell’operazione 42$^2$ = 1764.

2) Procedura algoritmica (variante della precedente): si assume come unità di misura non il lato del quadratino della quadrettatura (come nella procedura 1) ma il suo doppio; in questo caso non sono necessarie la moltiplicazione e la divisione per 2 e l’algoritmo diventa: 7$^2$ =4 9 (area del quadrato interno alla figura di posto 7), 49 × 9 = 441 (area del quadrato interno alla figura cercata), √441 = 21 (posto della figura cercata). Questa procedura spesso non è stata riconosciuta dai correttori.

3) Procedura basata sul rapporto di similitudine: in pochi casi si osserva, dai disegni proposti nel testo, che l’area della figura di posto 3 è 9 volte quella della figura di posto 1; ciò porta ad intuire o a ricordare che, se il lato triplica, l’area diventa 9 volte e ad arrivare brevemente alla soluzione 7 × 3 = 21.

4) Procedura per elencazione: vengono calcolate tutte le aree dei quadrati da quello della figura di posto 1 a quello della figura di posto 21.

Errori

1) Errori in qualche passaggio della procedura algoritmica 1:

a. Dimenticanza della divisione finale per 2

b. Sostituzione dell’operazione di radice quadrata con una divisione per 2

c. Sostituzione della moltiplicazione per 9 con una addizione di 9

2) Errata applicazione del rapporto di similitudine (errore frequente): si ipotizza che, se l’area è 9 volte rispetto alla figura di posto 7, anche il lato del quadrato interno e quindi il posto siano anch’essi 9 volte, arrivando alla soluzione 7 × 9 = 63.

3) Combinazione dei precedenti errori 1c e 2: si aggiunge 9 al posto 7 ottenendo 7+9=16

4) Individuazione di una relazione ricorsiva errata fra i termini della successione, dedotta dai primi tre termini

Indicazioni didattiche

Il problema si è rivelato interessante e coinvolgente per gli allievi, come dimostra lo scarso numero, in tutte le categorie, di elaborati privi di svolgimento. Quasi tutti presentano qualche calcolo o disegno o traccia di ragionamento descritto a parole.

Sicuramente, dal punto di vista didattico, l’interesse è focalizzato sulla presenza di quantità variabili e sulle loro relazioni. Le variabili sono molteplici ma solo tre hanno interesse per il problema: il posto della figura, il lato del quadrato grigio interno alla figura e l’area di questo quadrato; la loro individuazione rispetto ad altre variabili, come gli elementi del quadrato esterno o le parti bianche della figura, rappresenta un primo importante passo nella fase di appropriazione della situazione e può essere oggetto di un’attività di discussione in classe.

Una volta messa a fuoco la presenza di una successione di numeri (le misure delle aree) dipendenti da altri numeri (i posti), un elemento di discussione in classe può essere il confronto fra le varie strategie, finalizzato a comprendere che non è necessario elencare tutti i termini della successione (procedura 4) ma che ci si può concentrare sui due termini interessati (procedure 1, 2, 3). Il passaggio dal posto 7 al posto 21 può avvenire in vari modi ed utilizzando diversi registri, che è utile mettere a confronto: da una descrizione a parole, all’utilizzo di una sequenza di operazioni e delle loro inverse (algoritmo), fino ai tentativi di introdurre scritture simboliche. Anche se per la risoluzione di questo problema non è necessario, si può lavorare in classe sullo sviluppo di tali scritture, fino ad arrivare ad una formula che lega il posto della figura n, con l’area del quadrato grigio interno A(n). A proposito dell’area, il problema può essere anche l’occasione per convincersi che si possono utilizzare diverse unità, tutte ugualmente lecite, per misurarla.