Une spirale particulière (bis)

Identification

Rallye: 31.II.13 ; catégories: 6, 7, 8, 9, 10 ; domaine: FN
Familles:

• PRG - Traiter des progressions
• PRG/PA - Traiter des progressions arithmétiques

Envoyer une remarque ou une suggestion

Résumé

Calculer la somme des 50 premiers termes de deux progressions arithmétiques alternées (1 + 2 + ... + 23 + 24 + 25) + (5 + 6 + 7 + … + 28 + 29), à partir du dessin d’une « spirale » sur quadrillage.

Enoncé

Tâche de résolution et savoirs mobilisés

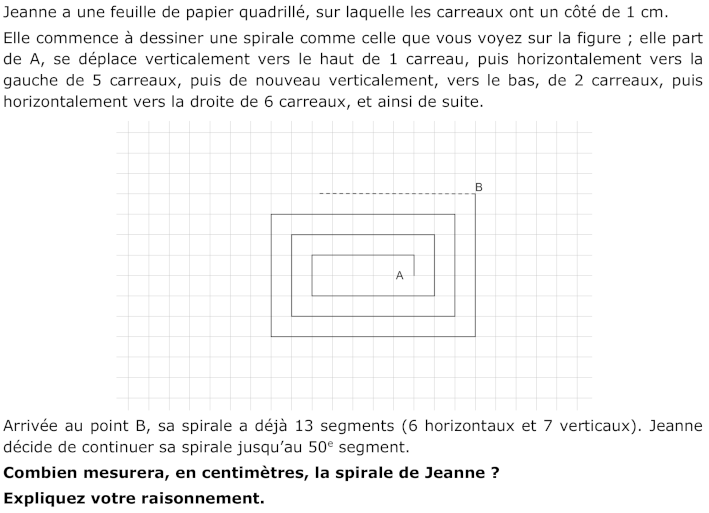
Observer la spirale et comprendre les règles de sa construction : les mesures des segments en cm, aussi bien horizontaux que verticaux, augmentent chaque fois de 1 cm. La prolonger éventuellement de quelques segments.

Les connaissances nécessaires se limitent à l’addition et une mise en œuvre de ses propriétés.

- Constater qu’il y aura 25 segments verticaux et 25 horizontaux. Déterminer la mesure des segments verticaux est 1, 2, 3, 4, ... , 25, celle des segments horizontaux 5, 6, 7, 8, 9, … , 29 et qu’il s’agira d’additionner ces 50 nombres.

- Pour éviter l’addition des 50 termes il est possible de les regrouper par commutativité, associativité et distributivité.

Par exemple (1 + 5) + (2 + 6) … conduit à une addition de 25 termes : 6 + 8 + … + 52 + 54 puis un regroupement des termes (6 + 54) + (8 + 52) + (10 + 50) conduit à 60 + 60 + 60 + … + 60 + 30 = 12  60 + 30 = 750

- Il y a évidemment de nombreuses autres manières d’arriver à la longueur de la spirale

Notions mathématiques

progression arithmétique, terme, somme des termes,

Résultats

20.I.15

Points attribués sur 3789 classes de 21 sections:

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Réponse correcte « 750 cm » avec explications claires (calculs détaillés, inventaire des longueurs de segments, ...)
• 3 points: Réponse correcte avec explications sans le détail des nombres à additionner
  ou réponse avec une seule erreur (oubli ou confusion d’un terme, erreur de calcul)
• 2 points: Réponse correcte sans explication ni détails des nombres à additionner
  ou réponse avec deux ou trois erreurs (oubli ou confusion de deux ou trois termes, erreurs de calcul)
• 1 point: Début de raisonnement correct ou réponse avec plus de trois erreurs
• 0 point: Incompréhension du problème

Procédures, obstacles et erreurs relevés

Cette nouvelle version du problème semble un peu plus accessible que l'ancienne Une spirale particulière (20.I.15,cat 7 - 10)

Il faudra examiner les copies rendues par les groupes pour pouvoir en dire plus sur les obstacles,