Piramidi di cubi

Identificazione

Rally: 31.II.17 ; categorie: 8, 9, 10 ; ambiti: FN, OPN
Famiglie:

• SF - Studiare successioni di figure
• SN - Gestire una successione numerica
• VS/OA - Contare oggetti nello spazio

Envoyer une remarque ou une suggestion

Sunto

Osservare una successione regolare di costruzioni (“piramidi” di cubi), trovare la progressione del numero di cubi da una piramide alla seguente, poi la loro somma e determinare quante se ne possono costruire con 2000 cubi a disposizione.

Enunciato

Compito per la risoluzione e saperi mobilizzati

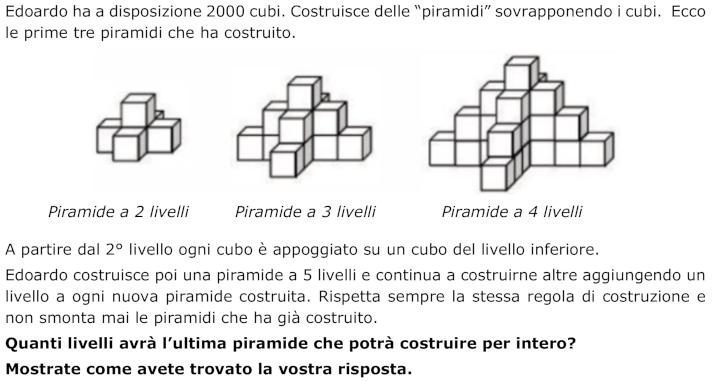
- Osservare le tre prime piramidi e comprendere che per passare da una piramide alla seguente si aggiungono i cubi del livello inferiore.

- Determinare il numero di cubi di ogni livello a partire dall’alto e trovare di quanto aumenta il numero di cubi da una piramide all’altra, cioè scoprire la progressione aritmetica 1; 5 ; 9 ; 13 ; 17 ; 21 ; … di ragione 4.

- Passare al numero di cubi di ogni piramide e scoprire la progressione 6 (1 + 5); 15 (6 + 9) ; 28 (15 + 13) …

- Passare al numero di cubi delle prime piramidi: 6; 21 (6 + 15); 49 (21 + 28); 94; (49 + 45) …

- Il calcolo di questi numeri successivi fa parte del compito ed esige un’organizzazione e una disposizione precise che ci si può aspettare da alunni di queste categorie. Quelli che sanno utilizzare un foglio di calcolo sono avvantaggiati! Tre successioni di numeri corrispondono a funzioni definite in N dove n è il numero di livelli della piramide.

- La prima è la funzione lineare n –> 4 (n – 1) + 1, è facilmente accessibile

- La seconda è una funzione di secondo grado n –> n(2n - 1), più difficile da trovare

Riportiamo qui sotto una tabella riassuntiva per aiutare le persone che devono attribuire i punteggi:

  nb dinivelli           2   3   4   5   6   7   8   9  10  11   12   13   14   15
  cubi/livello aggiunto  5   9  13  17  21  25  29  33  37  41   45   49   53   57
  cubi/piramide          6  15  28  45  66  91 120 153 190 231  276  325  378  435
  totale dei cubi        6  21  49  94 160 251 371 524 714 945 1221 1546 1924 2359

Nozioni matematiche

progressione, sequenza, piramide, cubi, somma, numero naturale

Risultati

31.II.17

Punteggi attribuiti su 1186 classi di 20 sezioni:

Secondo i criteri dell’analisi a priori :

• 4 punti: Risposta corretta “14 livelli” con descrizione completa del procedimento seguito (presenza di disegni e/o calcoli e/o tabelle che portano alla risposta)
• 3 punti: Risposta corretta con spiegazioni poco chiare o non sufficientemente dettagliate
  oppure risposta (13 o 15 livelli) con descrizione
• 2 punti: Risposta corretta senza spiegazione
  oppure procedimento corretto con risposta sbagliata dovuta a uno o più errori di calcolo
  oppure risposta (12 o 16 livelli) con descrizione
• 1 punto: Inizio di procedimento corretto (determinazione del numero di cubi utilizzati per costruire le prime tre piramidi (49) e comprensione della regola di passaggio da una piramide alla seguente)
  oppure risposta 21 livelli per non aver tenuto conto del fatto che le piramidi già costruite non vengono disfatte (costruzione di un’unica piramide avendo a disposizione 2000 cubetti, seguendo le regole di costruzione)
• 0 punto: Incomprensione del problema