
Banca di problemi del RMT
gm31-it
 |
Banca di problemi del RMTgm31-it |
|
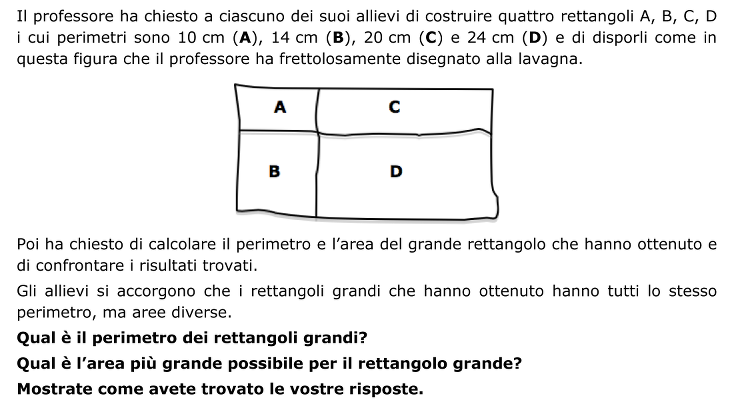
Formare rettangoli ognuno dei quali è composto da quattro rettangoli di perimetro dato (10, 14, 20 e 24 cm), trovare il perimetro e individuare quello con l’area maggiore.
Analisi a priori:
- Osservare la figura e comprendere perché ci possono essere rettangoli diversi con lo stesso perimetro di 10, 14, 20, 24 cm (possono essere tutti “allungati” e anche trasformati in quadrati).
- Comprendere che se si sceglie una lunghezza per uno dei lati del rettangolo con il perimetro di 10 cm, la lunghezza dell’altro lato è determinata e può essere calcolata sapendo che il perimetro è la somma delle lunghezze dei quattro lati, due lunghezze e due larghezze, per esempio
- Accorgersi che tutte le dimensioni degli altri tre rettangoli piccoli e di quello grande sono anch’esse determinate dal valore scelto per le dimensioni del primo rettangolo piccolo.
- Per rispondere alle due domande sul perimetro e l’area i calcoli possono per esempio essere raggruppati in modo ordinato a partire da una dimensione del primo rettangolo (perimetro 10 cm).

e constatare che il perimetro resta costante e che l’area aumenta e diminuisce in modo “simmetrico” rispetto al 72 dei valori di 3 e di 3,5, per comprendere che è necessario inserire un nuovo valore 3,25:
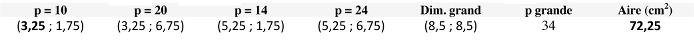
Constatare allora, vista la “simmetria” delle variazioni (aumenti seguiti da corrispondenti diminuzioni) che il più grande rettangolo ha un’area di 72,25 cm2.
- Si può arrivare a questa conclusione anche sapendo che tra tutti i rettangoli che hanno un perimetro di 34 cm, è il quadrato con il lato di 8,5 cm che ha l’area maggiore.
Oppure
- Risolvere il problema con la ricerca del massimo per la funzione A = x (17 – x) in cui la variabile è il primo lato di un rettangolo con il perimetro di 34 cm.
quadrato, rettangolo, perimetro, lunghezza, lato, divisione, addizione
Punti attribuiti su 1211 classi di 18 sezioni:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 8 | 205 (25%) | 401 (49%) | 116 (14%) | 79 (10%) | 10 (1%) | 811 | 1.12 |
| Cat 9 | 55 (26%) | 89 (43%) | 27 (13%) | 33 (16%) | 4 (2%) | 208 | 1.24 |
| Cat 10 | 44 (23%) | 82 (43%) | 28 (15%) | 31 (16%) | 7 (4%) | 192 | 1.35 |
| Totale | 304 (25%) | 572 (47%) | 171 (14%) | 143 (12%) | 21 (2%) | 1211 | 1.18 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
première analyse de (101 copies de FC)
Une majorité des groupes a trouvé le périmètre 34 à partir d’un seul essai de valeurs des côtés du rectangle de 10 cm de périmètre : en général 2 et 3. Dans un cas l’aire du grand rectangle est 66, dans l’autre cas 72 et c’est la valeur qui a été compris comme la plus grande aire.
Quelques groupes ont vérifié le périmètre 34 à partir de deux essais : 2 ; 3 et 1 ; 4
Seuls deux copies font état d’essais avec des mesures non entières :3,5 et 1, 5 et 4,5 et 0,5.
Quelques réponses ont conduit à 70 pour l’aire du grand rectangle, à partir de l’essai 4 ;1.
Seuls deux groupes ont perçu la classe des rectangles de périmètre 34 :
- La plus grande aire est 72,2499 cm. Pour trouver, on a, à partir du périmètre, fait des essais avec des longueurs et largeurs les plus rapprochées. Le périmètre étant 34 cm, on a pris comme longueur 8,51 cm et comme largeur 8,49 cm. On les a multipliés et le résultat était 72,2499 cm. On a essayé avec des valeurs plus éloignées et l’aire inférieure à celle de 72,2499. On remarque que, pour ces élèves, le carré (de côté 34/4 ou 8,5) n’appartient pas à la classe des rectangles.
- Comme pour le rectangle A, nous avons divisé le périmètre par 2 pour trouver sa moitié. On sait que la longueur × largeur = aire du rectangle, (34 :2 = 17). Si on prend deux chiffres qui donnent 17 une fois additionnés. par tâtonnements on commence par 2 et 15 (qui font 17) on fait 2× 15 = 30, on essaye d’autres possibilités comme 4 × 13= 52 ; 6× 11= 66, on voit que plus l’écart entre les deux chiffres est faible plus l’aire est grande. On décide de prendre la moitié de 17 (8,5) puisqu’on a pris la moitié de 17, l’écart est nul, on fait 8,5× 8,5 ce qui donne 72,25. La plus grande aire possible de ce rectangle est 72,25 cm2.
Il y a de nombreuses incompréhensions de « grand rectangle » de l’énoncé. Pour les adultes il s’agit de la réunion des quatre rectangles A, B, C, D, mais pour certains élèves, il s’agit de D (le plu grand sur la figure) ou des autres rectangles aussi puisque leur aire dépend des valeurs choisies pour les mesures des côtés.
Obstacles. La majorité de 0 pt et 1 pt révèle que le problème présente des obstacles importants. Nous avons vu que la recherche du maximum n’est pas possible si les rectangles de 34 cm de périmètre ne sont pas conçus comme appartenant à un classe d’une infinité de rectangles mais comme un ou deux cas particuliers. Mais si on se limite à la recherche du périmètre du grand rectangle, on constate 25% d’échecs.
Il y a encore des confusions entre aire et périmètre, des difficultés à utiliser les relations d’égalités entre côtés de rectangles contigus et, surtout une conception du périmètre comme somme de longueurs des côtés qui se limitent à ceux dont les mesures sont entières.
(c) ARMT, 2019-2024