Fili tesi

Identificazione

Rally: 24.F.23 ; categoria: 5 ; ambiti: GP, GM
Famiglie:

• IF - Identificare figure
• LA - Utilizzare misure di lunghezze e aree
• QUA - Lavorare su una quadrettatura
• QUA/GQ - Gestire poligoni su carta quadrettata

Remarque et suggestion

Sunto

Disegnare quadrati e rettangoli i cui i vertici si trovano su uno dei nodi di ciascuno dei quattro lati di una griglia a maglia quadrata 5 × 5 (ad eccezione dei nodi corrispondenti ai quattro vertici della griglia).

Enunciato

Compito per la risoluzione e saperi mobilizzati

- Osservare la figura B, capire che l’elastico è teso su quattro chiodi e che è la scelta dei chiodi che determinerà le forme dei quadrilateri.

- Per la ricerca dei quadrati, constatare che, poiché non ci sono chiodi sugli angoli della griglia (quadrato), occorre rinunciare al quadrato costituito dalla cornice della griglia, constatare poi che, se si scelgono dei chiodi sui due lati opposti, il quadrilatero avrà due lati più lunghi degli altri per immaginare infine dei quadrati i cui lati non siano paralleli a quelli della cornice (« obliqui » rispetto ai lati del foglio). Scoprire infine i due tipi di quadrati, quelli determinati dal primo chiodo a partire dagli angoli della griglia e quelli determinati dal secondo chiodo. Sulla figura C qui sotto: (1 ; 5 ; 9 ; 13) o (4 ; 8 ; 12 ; 16) e (2 ; 6 ; 10 ; 14) o (3 ; 7 ; 11 ; 15).

- Misurare i lati dei due tipi di quadrati per rendersi conto che i lati del primo tipo sono più lunghi di quelli del secondo tipo (la differenza è evidente, con un righello, o per riporto di segmenti). Colorare un quadrato di ciascun tipo, in rosso e in blu.

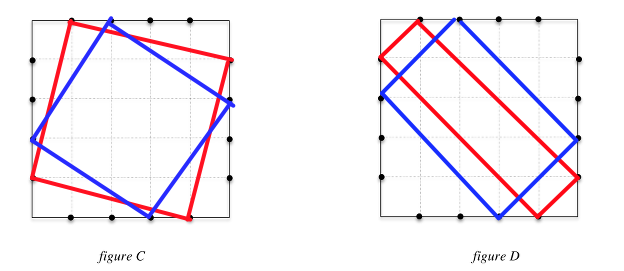
- Per la ricerca dei rettangoli, constatare che quelli che appaiono «spontaneamente», con i lati paralleli a quelli della griglia (o del foglio) non soddisfano il vincolo degli angoli su quattro lati diversi e dedurne che occorre cercare dei rettangoli disposti « obliquamente ».

- Per tentativi, scoprire i due tipi di rettangoli (1, 8, 9 ; 16) o (4, 5, 12 ; 13) e (2, 7, 10 ;15) o (3, 6, 11 ;14) (sulla figura D qui sotto) e confrontare le loro aree contando, per esempio, i quadrati della griglia in essi contenuti.

- Colorare in rosso il piccolo (1, 8, 9 ;16) o (4, 5, 12 ;13) l’area del quale è 8 quadrati della griglia, e in blu (2, 7, 10 ;15) o (3, 6, 11 ;14) l’area del quale è 12.

Nozioni matematiche

poligono, rettangolo, quadrato, perimetro, area, lunghezza, misura, lato, parallele, angolo dritto

Risultati

24.F.23

Points attribués, sur 12 copies de la 2e finale internationale du RMT (15.10.2016. Le locle)

I criteri di attribuzione dei punteggi sono i seguenti:

• 4 punti: Risposta corretta e completa : due quadrati e due rettangoli disegnati correttamente secondo il loro colore (v.figure C e D)
• 3 punti: I due quadrati e i due rettangoli disegnati correttamente ma con un’ inversione di colore
• 2 punti: I due quadrati e i due rettangoli disegnati correttamente ma con un’ inversione di colore in entrambi i casi
  oppure mancanza di un qudrato o di un rettangolo in un caso, con colori corretti nell’altro caso
  oppure uguaglianza dei due quadrati o dei due rettangoli, con colori corretti nell’altro cas
• 1 punto : Individuazione di un solo quadrato o un solo rettangolo, eventualmente con figure che non sono né rettangoli né quadrati
  oppure parallelogrammi che non sono né quadrati né rettangoli
• 0 punto: Incomprensione del problema: nessuna delle figure disegnate è un rettangolo o un quadrato o un parallelogramma

Procedure, ostacoli ed errori rilevati

- 4 classi su 12 hanno disegnato i due quadrati e i due rettangoli con i colori corretti (criterio d’attribuzione « 4 punti »)

- 4 classi hanno disegnato correttamente i quadrati ma hanno trovato solo uno dei due rettangoli richiesti, quello con l’area minore (8 quadrati della quadrettatura). La seconda figura è o un rettangolo due angoli del quale sono su uno stesso lato della griglia e lgli altri sul lato opposto della griglia o un parallelogramma.

- 1 classe ha disegnato correttamente i quadrati ma un parallelogramma e un quadrilatero irregolare al posto dei due rettangoli.

- 1 classe ha disegnato due quadrati, uno di 2x2 e l’altro di 3x3 quadrati interi della quadrettatura i cui angoli non sono sui lati della griglia; i due rettangoli sono disegnati correttamente.

- 2 classi non hanno rispettato il vincolo dei quattro angoli sui lati della griglia Globalmente, la percezione dei due quadrati è più agevole rispetto a quella dei due rettangoli.

Indicazioni didattiche

Questo problema di costruzione di figure su una cornice offre numerose indicazioni per tutti gli apprendimenti relativi alle proprietà dei poligoni attraverso la varietà di sviluppi possibili.

Le risposte alle due domande in effetti non sono che l’introduzione a numerosi altri problemi.

Per esempio, con le stesse condizioni (4 chiodi per lato ed un angolo su ciascun lato), riconoscere quadrilateri particolari:

• Quali sono i parallelogrammi (non rettangoli) che si possono formare?
• Quali sono i trapezi, isosceli, o no, che si possono formare?
• Si possono formare rombi non quadrati su questi chiodi?
• Si possono formare dei romboidi non quadrati su questi chiodi?
• Si possono formare dei quadrilateri che abbiano un solo angolo retto su questi chiodi?

Gli inventari:

• Quanti quadrilateri diversi (non isometrici o non esattamente sovrapponibili) si possono formare?
I calcoli dell’area, che fanno intervenire la sottrazione delle aree in quadrati della quadrettatura: a partire dall’area totale della griglia e dei quattro triangoli non compresi nei quadrilateri disegnati, situati nei quattro angoli della griglia:

• Quale può essere l’area di un quadrilatero costruito su questi chiodi, dalla più piccola alla più grande?
L’attività è facilmente realizzabile per manipolazione, con degli elastici su un geopiano o su una cornice semplice da costruire.

Gli allievi possono anche inventare nuove domande riguardo a questa griglia.

Per andare più lontano

La griglia 5x5 di questo problema naturalmente può essere modificata, la scelta dei chiodi anche, come i numeri di lati dei poligoni e le regole di posizionamento dei loro angoli.

Si giunge anche allo strumento geopiano, di una ricchezza inesauribile, che permette di esaminare tutti i concetti della geometria piana da costruire durante l’istruzione obbligatoria, con il supporto della manipolazione: poligoni, lunghezze, aree, angoli, parallelismo, perpendicolarità…

Bibliografia

Jaquet F.: 2016, 'Les problèmes de la deuxième finale internationale du RMT et leur analyse / I problemi della seconda finale internazionale del RMT e la loro analisi'. La Gazzetta di Transalpino / La Gazette de Transalpie no 6 pp.21-39.

(c) ARMT, 2016-2024