
Banque de problèmes du RMT
gp11-fr
 |
Banque de problèmes du RMTgp11-fr |
|
Envoyer une remarque ou une suggestion
Sur un quadrillage, déterminer les sommets manquants de rectangles dont certains sommets sont donnés, à partir d’un modèle placé dans une position différente.

Analyse a priori
Comprendre que les quatre pieds de la table forment une figure qui conserve ses propriétés métriques lors de déplacement (distance entre pieds et « angle » déterminé par 3 pieds consécutifs). Il s’agit d’imaginer la forme « rectangle » déterminée par ses quatre sommets sans le dessin des côtés.
Dès que la forme est reconnue, passer au dessin du rectangle dont les sommets sont les quatre cercles noirs de la position 1, puis procéder
Les solutions : 2 points rouges, 2 points bleus, 2 groupes de 3 points verts :
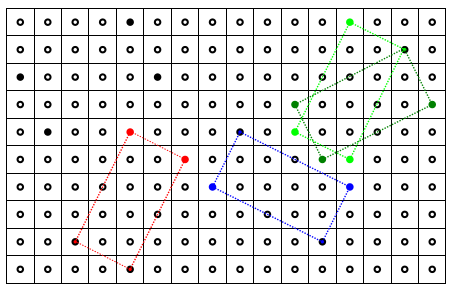
angle droit, rectangle, isométrie, longueur, comparaison, rotation, parallélogramme
Résultats des 12 classes de la finale internationale de 16e RMT (Brique 2008)
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 5 | 0 (0%) | 8 (67%) | 1 (8%) | 3 (25%) | 0 (0%) | 12 | 1.58 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
Résultats d'une expérimentation du problème dans 195 classes de 4 sections
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 5 | 5 (16%) | 16 (50%) | 7 (22%) | 4 (13%) | 0 (0%) | 32 | 1.31 |
| Cat 6 | 20 (29%) | 35 (51%) | 10 (15%) | 1 (1%) | 2 (3%) | 68 | 0.97 |
| Cat 7 | 19 (20%) | 35 (37%) | 23 (24%) | 10 (11%) | 8 (8%) | 95 | 1.51 |
| Total | 44 (23%) | 86 (44%) | 40 (21%) | 15 (8%) | 10 (5%) | 195 | 1.29 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
Voici les réponses obtenues pour la première dispositions de la table en "position rouge" par les 12 groupes d'élèves.
table en position « rouge »
a) 3 réponses correctes avec des-sin du rectangle
b) 1 réponse « légèrement décalée » ave dessin de la figure
c) 2 réponses avec un côté incliné à 45 degrés passant par quatre cercles, l’une avec figure, l’autre sans figure
d) 2 réponses « très décalées » l’une avec figure, l’autre sans figure
e) 4 réponses avec un côté isométrique et parallèle au côté du rectangle noir de la donnée, sans dessin de la figure.
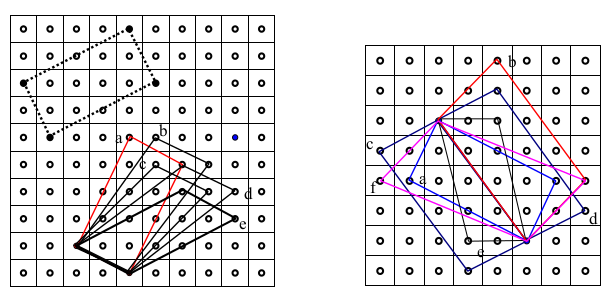
Les résultats sont tout à fait comparables pour la table en "position bleue" ou les tables en "position verte". Presque toutes les "tables dessinées" sont des parallélogrammes non rectangles.
Surpris par cette confusion systématique entre rectangle et parallélogramme non rectangle, le groupe de travail "géométrie plane" a conduit une expérimentation dans des classes de catégories 5 à 7 pour voir si l'erreur se retrouvait aussi avec des groupes d'élèves plus âgés.
Globalement les meilleurs résultats ont été obtenus dans des versions « guidées » où l'on demandait de déterminer d'abord seulement un des sommets manquants du « rectangle vert ». Si on considère cependant les résultats relatifs au seul « rectangle rouge », dans les catégories 6, 7 et 8, où elles ont été proposées individuellement sur environ 100 productions, les pourcentages de réussite varient très peu et tournent tous autour du 45 %. Dans le cas de la version version d'origine, sur une centaine d'élèves auxquels le problème avait été à nouveau proposé le pourcentage de réussite au « rectangle rouge » était de 43%.
Cette erreur systématique suggère une exploitation en classe de ce problème. On peut être certains que, entre les différents élèves d'une classe ou les différents groupes, vont apparaître des "tables" différentes qui vont permettre des confrontations et des échanges lors de mises en commun. Ce sera l'occasion de constater que l'angle droit doit être pris en compte dans un rectangle en position "inhabituelle", alors que cette propriété passe inaperçue dans les figures disposées avec leurs côtés parallèles au bord de la feuille.
Le problème se prête encore à de nombreux développements:
- Constater que, dans une rotation de 90 degrés, les côtés du rectangle suivent toujours les diagonales de rectangles du quadrillage de dimensions (1 x 2) et que ceci permet de vérifier que l'angle est droit si on imagine une rotation d'un quart de tour.
- Proposer aux élèves un rectangle de mêmes dimensions que celui de la table mais avec ses sommets sur les intersections du quadrillage au lieu des centres des carrés et demander de calculer son aire en carreaux du quadrillage: 10. (Ce qui peut se faire par comptage des 4 carreaux entiers et 6 carreaux reconstitués). Puis faire décomposer le rectangle en deux carrés égaux juxtaposés, dont l'aire est 5 en carreaux du quadrillage. Finalement, demander combien mesure le côté de ce carré (en côtés de carreau), en s'aidant de la calculatrice pour arriver progressivement à des approximations successives de 2; 2,1; 2,2: 2,3; 2,25; ... Ce développement permet de prendre en compte un nouveau nombre, qu'on ne peut pas déterminer par des mesures à la règle mais dont on peut s'approcher par élévations au carré et dont la calculatrice pdonne une bonne approximation par sa touche √.
- Il y a aussi tout le domaine des isométries à envisager: translations et rotations qui permettent de passer d'un rectangle à l'autre.
Ce problème a donné lieu à plusieurs expérimentations et analyses sur le thème de la reconnaissance du rectangle. Voir bibliographie Il rettangolo … non così evidente , avec la création de variantes et d'autres problèmes.
D'autres problèmes ont été élaborés à la suite de La table à déplacer: Les dix points (18.I.08), Le mur de l'école (I) (18.II.06), Le mur de l'école (II) (18.II.13)
On y trouve encore, en particulier, des considérations très importantes sur la formation du concept de rectangle dans les conclusions que nous nous permettons de citer ici:
... À un premier niveau, le rectangle est une forme plate que l’on rencontre souvent de face (une porte, une fenêtre,…) ou que l’on peut disposer devant soi bien droit (avec deux cotes verticaux). On reconnaît les rectangles à travers une perception globale : chaque rectangle en position privilégiée donne la sensation d’occuper l’espace de la même façon (…) Quelqu’un qui se trouve à ce stade de développement mental manie donc familièrement le rectangle, et éventuellement le nomme. Mais il n’est guère capable d’en parler, d’expliquer certains de ses caractères ou des phénomènes dont il est le siège.
Il s’agit ici du premier niveau, celui de préconcept.
À un deuxième niveaux, le rectangle s’installe davantage dans la conscience et le langage, également dans la volonté de connaître. Il est non seulement utilisé et nommé, mais on peut aussi parler de ses cotés horizontaux et verticaux, de l’égalité de ses côtés, de ses angles droits. (…) Ce niveau de connaissance du concept peut être plus ou moins développé, selon l’expérience de la personne, et en particulier selon son parcours scolaire. Les connaissances en question ont leur source dans les expériences sensori-motrices présentés au niveau précèdent. Mais elles manifestent un degré d’organisation mentale plus complexe. (…) En suivant Freudenthal [1983], nous appelons objets mentaux les concepts mobilisés à ce niveau de l’activité intellectuelle.
Passons maintenant à un troisième niveau, celui des mathématiques constituées. Là le rectangle n’est plus, comme les rectangles de notre environnement familier, un objet que l’on peut aborder, dont on peut se servir et auquel on peut réfléchir sans préalable. Il apparaît à sa place dans le déroulement d’une théorie, place variable selon les axiomes que l’on se donne. ( …) Le rectangle apparaît comme un épisode d’une entreprise intellectuelle exigeante et de longue haleine. (…) nous avons décidé d’utiliser, pour designer ce type de concepts, la locution de concepts formels.
Il apparaît alors clairement que “L’apprentissage des mathématiques consiste en un certain sens à passer…des préconcepts aux objets mentaux, puis éventuellement aux concepts formels. (…) Il n’y a pas de concept formel de rectangle qui n’ait ses racines dans le préconcept de rectangle et dans l’objet mental rectangle. Les trois niveaux des concepts sont sollicités dans la pensée mathématique créative. Les deux premiers sont surtout source d’images et d’intuitions, le dernier fournit les instruments de la rigueur.
À ce stade, le titre de notre article « le rectangle… pas si évident ! » commence à avoir sa raison d'être....
Exemples d'activités en vue d'un parcours didactique avec la classe
À expérimenter en classe, selon des modalités déterminées par l'enseignant; avec envoi de description et commentaires pour rendre compte de l'opportunité de l'activité pour la construction des savoirs (notés en italique).
a) Après le débat collectif où les tables ont été reconnues "correctes" (rectangles et non "parallélogrammes non-rectangles"), faire dessiner le carrelages du sol de la cuisine sur papier quadrillé avec des carreaux de 1 cm de côté, puis demander combien de tables pourrait-on y disposer au maximum, de mêmes dimensions que celle de l'énoncé, qui ne se touchent pas et qui ont toutes les quatre pieds sur quatre petits cercles du carrelage, enfin dessiner les rectangles de ces tables.
Savoir que, dans une situation comme celle-ci, la manipulation n'est pas interdite mais au contraire vivement recommandée. Autres savoirs: dessin sur quadrillage, parallèles et perpendiculaires, segments isométriques (diagonales de rectangles 1 x 2), longueur double de la largeur, centre des carreaux, décomposition du "rectangle-table" en deux carrés, reports, recouvrement optimal, ...
b) Combien mesure, en cm, la diagonale d'une des tables (rectangle) que vous avez dessinées sur laquelle se situent 6 petits cercles ? combien mesure l'autre diagonale de cette table, celle sur laquelle il n'y a que 2 petits cercles: ceux des extrémités.
Un savoir qui fait partie des propriétés du rectangle pour les mathématiciens: mais qui, vu la position particulière des tables est vraisemblablement encore ignoré de beaucoup d'élèves et adultes : les deux diagonales d'un rectangle sont isométrique ! Un débat collectif s'annonce passionnant pour estimer le niveau de conviction de cette isométrie, même à partir de découpages ou autres manipulations où ces deux diagonales se correspondent matériellement.
c) Coupez en deux le rectangle d'une table pour en faire deux triangles égaux. Juxtaposez ces deux triangles par un côté entier. Combien de figures peut-on obtenir ainsi, en plus du rectangle d'origine ?
Découverte de deux triangles isocèles et d'un quadrilatère "cerf-volant".
d) Conservez un des deux triangles égaux précédents et découpez l'autre en deux parties pour former, avec ces trois pièces un nouveau rectangle dont la mesure de la largeur et de la longueur est un nombre entier de cm (mesure du côté d'un carreau du carrelage); puis calculez son aire.
Savoir que ce nouveau rectangle a une aire de 10 cm$^2$, comme celle du rectangle d'une table et que, par conséquent la table peut de décomposer en deux carrés de 5 cm$^2$.
e) Quelles sont les dimensions (largeur et longueur) du rectangle d'une table et combien mesure le côté d'un carré "demi-table" ?
Savoirs: ces dimensions ne sont pas des nombres entiers! Ce ne sont pas des nombres décimaux! Ce ne sont pas des nombres rationnels - qu'on peut écrire sous forme de fraction avec deux nombres entiers. (la calculatrice ne peut pas les afficher, elle n'en propose que des approximations. L'enseignant doit alors "informer" les élèves que ces nombres s'écrivent avec le symbole √ : √5 et 2x√5 ou √20. Eventuellement dire qu'en mathématiques on les appels "nombres irrationnels", mais sans insister.
f) Autres problèmes de la banque cités ci-dessus.
Salin, M.-H. (2008). Enseignement et apprentissage de la géométrie à l’école primaire et au début du collège : le facteur temps. Bulletin vert de l'APMEP, no 478, 647-670.
Jaquet F. (2009). La finale internazionale du 16e RMT, problèmes et analyse. In L. Grugnetti, F. Jaquet (Eds) Rally Matematico Transalpino e intercultura, ARMT, SCNAT, 225-253.
Anselmo B., Bisso C., Grugnetti L. (2011). Il rettangolo … non così evidente. Gazzetta di Transalpino, n° 1 [[http://bprmt.projet-ermitage.org/gazette/Gazzetta-01.pdf]]