Il tavolo da spostare

Identificazione

Rally: 16.F.24 ; categorie: 4, 5 ; ambito: GP
Famiglie:

• ANG - Utilizzare angoli e/o misure di angoli
• IF - Identificare figure
• IF/RC - Riconoscere e costruire figure elementari
• QUA - Lavorare su una quadrettatura
• QUA/GQ - Gestire poligoni su carta quadrettata

Remarque et suggestion

Sunto

Su una quadrettatura, determinare i vertici mancanti di rettangoli nei quali alcuni vertici sono dati, a partire da un modello sistemato in una posizione diversa

Enunciato

Compito per la risoluzione e saperi mobilizzati

Analisi da priori

Capire che i quattro piedi del tavolo formano una figura che conserva le sue proprietà metriche all’atto degli spostamenti (distanza tra i piedi e “angoli” determinati da 3 piedi consecutivi). Si tratta di immaginare la forma «rettangolo» determinata dai suoi quattro vertici senza il disegno dei lati.

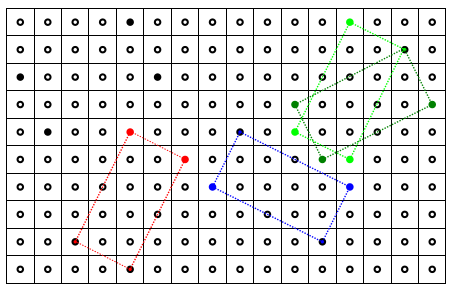
Una volta riconosciuta la forma, passare al disegno del rettangolo i cui vertici sono i quattro cerchietti neri della posizione 1, poi procedere:

• sia con ritaglio e spostamento del pezzo rettangolare
• sia con la costruzione di altri rettangoli con il righello (tramite la misura delle lunghezze dei lati o con il riporto) e uso della squadra per gli angoli retti o ancora sistemando una diagonale, orizzontale o verticale, su 6 cerchietti
• sia visivamente con il conteggio o facendo riferimento ai cerchietti con spostamenti di 1 (o 2) verticalmente e di 2 (o 1 orizzontalmente); o ancora osservando che una diagonale è formata da 6 cerchietti allineati orizzontalmente o verticalmente.

Le soluzioni: 2 cerchietti rossi, 2 cerchietti blu, 2 gruppi di 3 cerchietti verdi.

Nozioni matematiche

angolo retto, rettangolo, isometria, lunghezza, confronto, rotazione, parallelogramma

Risultati

16.F.24

Risultati delle 12 classi della finale internazionale del 16° RMT (Briga 2008)

Sperimentazione

Résultats d'une expérimentation du problème dans 195 classes de 4 sections

Secondo i criteri di attribuzione dei punteggi:

• 4 punti: Risposta corretta e completa: i due cerchietti (o punti) rossi, 2 blu e 6 (2 x 3) verdi, con individuazione delle quattro posizioni del tavolo, con o senza il disegno dei lati del rettangolo fittizio
• 3 punti: Una delle quattro posizioni del tavolo non è determinata, ma le altre tre lo sono con la posizione dei piedi
  oppure le quattro posizioni sono determinate ma con la deformazione di una delle figure
• 2 punti: Due delle quattro posizioni del tavolo non sono determinate, ma le altre due lo sono con la posizione dei piedi
  oppure tre posizioni determinate ma con una deformazione di una delle figure
• 1 punto: Una sola posizione correttamente determinata
  oppure nessuna posizione interamente corretta, ma con delle deformazioni
• 0 punto: Incomprensione del problema

Procedure, ostacoli ed errori rilevati

Ecco le risposte ottenute per la prima disposizione del tavolo in posizione “rosso” per i 12 gruppi di allievi

a) 3 risposte corrette con disegno del rettangolo

b) 1 risposta “leggermente spostata” con disegno della figura

c) 2 risposte con un lato inclinato a 45 gradi passante per quattro cerchietti, l’uno con figura, l’altro senza figura

d) 2 risposte “molto spostate” l’una con figura, l’altra senza figura

e) 4 risposte con un lato congruente e parallelo al lato del rettangolo nero del dato, senza disegno della figure.

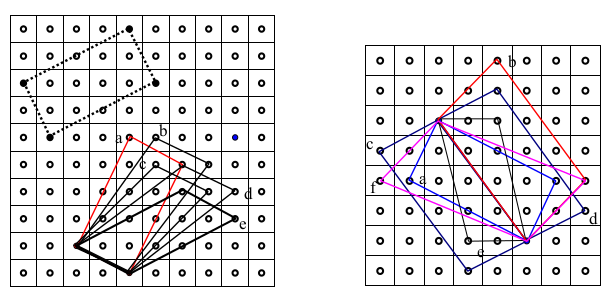
I risultati sono sostanzialmente confrontabili per il tavolo in “posizione blu” o i tavoli in “tavoli verde”. Quasi tutti i “tavoli disegnati” sono dei parallelogrammi non rettangoli

I riferimenti alle misure dei lati non sono numerosi:

- I tavoli si sono disposti tutti in parti oblique e abbiamo trovato questa risposta facendo cosi: la base minore misurava 2,3 cm e la base maggiore misurava 4,5 cm. Noi abbiamo seguito i dati e cosi ci è venuto fuori i 5 tavoli (che non era comunque dei rettangoli).

- Si può spostare 4 volte il tavolo. Abbiamo misurato i punti neri. Quindi abbiamo preso gli altri con le “masse” dei punti neri. Perché c’è sempre lo stesso tavolo, non può diventare più grande né più piccolo! L’altezza è 2,2 cm, la lunghezza è 4,5 cm e di traverso in alto c’è 5 cm.). (Le misure sono indicate bene con doppie frecce. Tre configurazioni in forma di parallelogramma non rettangoli sono disegnati: una con punti rossi, una di punti blu e una di punti verdi).

- Si può spostare 4 volte il tavolo. Abbiamo misurato i punti neri. Quindi abbiamo preso gli altri con le «masse» dei punti neri. Perché c’è sempre lo stesso tavolo, non può diventare più grande né più piccolo! L’altezza è 2,2 cm, la lunghezza è 4,5 cm e di traverso in alto c’è 5 cm. (Le tre misure sono ben indicate da doppie frecce)

Sorpreso da questa confusione sistematica tra rettangolo e parallelogramma non rettangolo, il gruppo di lavoro “geometria piana” ha condotto una sperimentazione in classi di categoria 5, 6 e 7 per vedere se l’errore si ritrovasse anche con gruppi di allievi più grandi, come riportato in Anselmo, Bisso, Grugnetti (2011).

Globalement les meilleurs résultats ont été obtenus dans des versions « guidées » où l'on demandait de déterminer d'abord seulement un des sommets manquants du « rectangle vert ». Si on considère cependant les résultats relatifs au seul « rectangle rouge », dans les catégories 6, 7 et 8, où elles ont été proposées individuellement sur environ 100 productions, les pourcentages de réussite varient très peu et tournent tous autour du 45 %. Dans le cas de la version version d'origine, sur une centaine d'élèves auxquels le problème avait été à nouveau proposé le pourcentage de réussite au « rectangle rouge » était de 43%.

Indicazioni didattiche

Questo errore sistematico suggerisce una utilizzazione in classe di questo problema. Si può essere certi che, tra i diversi allievi di una classe o i diversi gruppi, appariranno “tavoli” differenti che permetteranno un confronto e scambi all’atto della messa in comune. Sarà l’occasione per constatare che bisogna tener conto dell’angolo retto in un rettangolo in posizione “inabituale”, mentre tale proprietà passa inosservata nelle figure disposte con i lati paralleli ai bordi del foglio.

Il problema si presta a numeri altri sviluppi:

- Constatare che in una rotazione di 90 gradi i lati del rettangolo seguono sempre le diagonali di rettangoli della quadrettatura di dimensioni (1 x 2) e che ciò consente di verificare che l’angolo è retto se si immagina una rotazione di un quarto di giro.

- Proporre agli allievi un rettangolo avente le stesse dimensioni di quelle del tavolo, ma con i vertici sulle intersezioni della quadrettatura invece che al centro dei quadratini e chiedere di calcolare la sua area in quadratini della quadrettatura: 10 (cosa che può farsi con conteggio dei 4 quadratini interi e di 6 ricostituiti). Poi far scomporre il rettangolo in due quadrati uguali giustapposti, la cui area è 5 in quadratini della quadrettatura. Infine, chiedere quanto misura il lato di questo quadrato (in lati dei quadratini).

Aiutandosi con la clacolatrice per arrivare progressivamente a approssimazioni successive di 2; 2,1; 2,2; 2,3; 2,25; ... Questo sviluppo permette di considerare un “nuovo” numero che non si può determinare con misure tramite il righello ma che ci si può avvicinare con elevamento al quadrato e di cui la calcolatrice dà una buona approssimazione con il tasto √.

- C’è anche da pensare all’ambito delle isometrie: traslazioni e rotazioni che permettono di passare da un rettangolo all’altro.

Per andare più lontano

Questo problema ha dato luogo a diverse sperimentazioni e analisi sul tema del riconoscimento del rettangolo. Si veda in bibliografia Il rettangolo … non così evidente, con la creazione di varianti e di altri problemi: I dieci punti (18.I.08), Il muro della scuola (I) (18.II.06), Il muro della scuola (II) (18.II.13).

Nelle conclusioni dell’articolo citato, che ci permettiamo di riportare qui di seguito, si trovano anche, in particolare, considerazioni molto importanti sulla formazione del concetto di rettangolo:

“Ad un primo livello, il rettangolo è una forma piatta che incontriamo sovente di fronte (una porta, una finestra, ...) o che possiamo disporre davanti a noi “ben dritta” (con due lati verticali). Riconosciamo il rettangolo attraverso una percezione globale: ogni rettangolo in posizione privilegiata dà la sensazione di occupare lo spazio nello stesso modo (...) Chi si trova a questo stadio di sviluppo mentale ha dunque familiarità̀ con il rettangolo, ed eventualmente gli dà un nome. Ma non è per nulla capace di parlarne, di spiegare alcune delle sue caratteristiche o fenomeni che gli sono propri.” Si tratta qui del primo livello, quello di pre-concetto.

“Ad un secondo livello, il rettangolo si installa meglio nella coscienza e nel linguaggio, ed anche nella volontà̀ di conoscere. Non è solamente utilizzato e nominato, ma si può̀ parlare dei lati orizzontali e verticali, dell’uguaglianza dei lati, degli angoli retti (...) Questo livello di conoscenza del concetto può̀ essere più̀ o meno sviluppato, secondo l’esperienza della persona, e in particolare secondo il suo percorso scolare. Le conoscenze in questione hanno la loro sorgente nelle esperienze sensorie-motrici presentate al livello precedente. Ma esse indicano un grado di organizzazione mentale più̀ complesso. (...) Seguendo Freudenthal [1983], diciamo oggetti mentali i concetti mobilizzati a questo livello dell’attività̀ intellettuale.”

“Passiamo ora ad un terzo livello, quello della matematica costituita. Qui il rettangolo non è più̀, come i rettangoli dell’ambiente intorno a noi, un oggetto che si possa approcciare, di cui ci si possa servire e sul quale si possa riflettere senza uno studio anteriore. È al suo posto nello sviluppo di una teoria, posto che varia a secondo degli assiomi che ci si dà. (...) Il rettangolo appare come un episodio di un’impresa intellettuale esigente e di lungo respiro. (...) abbiamo deciso di utilizzare, per designare questo tipo di concetti, la locuzione concetti formali.”

E viene allora chiarito che “L’apprendimento della matematica consiste in un certo senso nel passare...dai pre- concetti agli oggetti mentali, poi eventualmente ai concetti formali. (...) Il concetto di rettangolo matematico ha le sue radici nel pre-concetto di rettangolo e nell’oggetto mentale rettangolo. Tutti e tre i livelli dei concetti sono sollecitati nel pensiero creativo. I primi due sono soprattutto sorgente di immagini e intuizioni, l’ultimo fornisce gli strumenti del rigore.” A questo punto, il titolo del nostro rapporto “Il rettangolo...non così evidente!” comincia ad avere una sua ragion d’essere.

Bibliografia

Anselmo B., Bisso C., Grugnetti L. (2011). Il rettangolo…non così evidente Gazzetta di Transalpino, n. 1, sito dell’ARMT: http://www.armtint.org/fr/le-gazzette-di-transalpino/numero-1/viewcategory/12-gazzetta-n-1-articoli/

Jaquet F.: 2009, ‘La finale internazionale du 16e RMT, problèmes et analyse’, in L. Grugnetti, F. Jaquet (Eds) Rally Matematico Transalpino e intercultura, ARMT, SCNAT, 225-253.

Salin, M-H.: 2008, ‘Enseignement et apprentissage de la géométrie à l’école primaire et au début du collège, le facteur temps’, APMEP, n. 478, 647-670.

(c) ARMT, 2008-2024