
Banca di problemi del RMT
gp116-it
 |
Banca di problemi del RMTgp116-it |
|
A partire dal disegno di un pavimento rettangolare di 15 metri di perimetro, ricoperto da mattonelle rettangolari uguali fra loro di cui è noto il prezzo al metro quadrato, calcolare la spesa per l’acquisto di tutte le mattonelle.
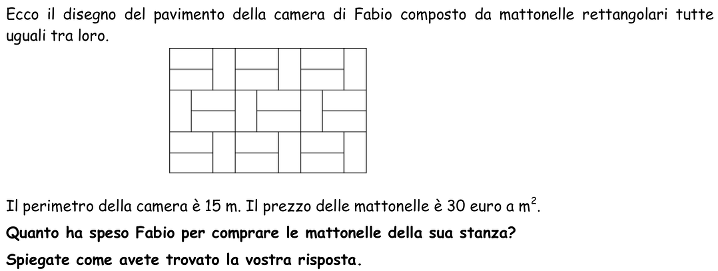
- A partire dalla lettura del testo capire che è necessario calcolare l’area del pavimento (rettangolo) per poter rispondere alla domanda relativa al prezzo.
- Osservare la figura e coglierne le regolarità sia orizzontalmente che verticalmente.
- Vedere (dall’accostamento delle mattonelle rettangolari) che la lunghezza delle mattonelle è il doppio della larghezza e che questa è la “relazione-chiave” della situazione che permette di definire un’unità comune per la misura dei lati.
Per esempio, prendendo la larghezza di una mattonella come unità o immaginando una trama quadrettata sulla pavimentazione con ogni mattonella che ricopre 2 quadretti unità della trama, le dimensioni della stanza sono 9 e 6 e il perimetro 30, in lati del quadretto-unità.
- Per proporzionalità trovare le misure in metri: dalle misure del perimetro nelle due unità, 30 (in lati di quadretti-unità) e 15 (in m), si determina il rapporto 15/30 oppure 1/2 o 0,5 che indica la misura in metri del lato di una mattonella, quindi le dimensioni della stanza sono 4,5 e 3 (in m).
- Calcolare allora all’area del pavimento: 3 × 4,5 = 13,5 (in m2) e il prezzo delle mattonelle: 13,5 × 30 = 405 (in euro).
Oppure con una procedura algebrica:
esprimere le dimensioni con delle lettere (per esempio x e y per la larghezza e la lunghezza di una mattonella, poi sostituire y con 2x per arrivare all’equazione: 2(9x + 6x) = 15 da cui 30x = 15; x = 1/2; poi, come in precedenza, determinare le dimensioni di una mattonella, calcolare la sua area e il suo prezzo.
rettangolo, perimetro, lunghezza, larghezza, area, unità, piastrellatura, prezzo, proporzionalità
Punteggi attribuiti su 1175 classi di 19 sezioni:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 8 | 186 (23%) | 89 (11%) | 72 (9%) | 179 (22%) | 281 (35%) | 807 | 2.35 |
| Cat 9 | 24 (12%) | 12 (6%) | 21 (11%) | 51 (26%) | 88 (45%) | 196 | 2.85 |
| Cat 10 | 17 (10%) | 10 (6%) | 18 (10%) | 38 (22%) | 89 (52%) | 172 | 3 |
| Totale | 227 (19%) | 111 (9%) | 111 (9%) | 268 (23%) | 458 (39%) | 1175 | 2.53 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
Secondo i criteri dell’analisi a priori:
La procedura più comune è stata quella di ricercare una unità di misura comune nel perimetro: o il lato « lungo » della mattonella o il lato « corto » ; oppure cercare comunque dei « moduli » che si ripetono nella figura, molto comune la divisione nella griglia di quadratini aventi il lato uguale al lato corto della mattonella.
Meno presente il ragionamento sul rapporto 6 a 9 delle dimensioni del rettangolo grande.
Rarissime le procedure algebriche per gli elaborati di categoria 8.
- Nelle categorie 9 e 10 si utilizza il procedimento algebrico, ma non in maniera predominante e nella maggior parte dei casi traduce in linguaggio simbolico ciò che la maggior parte degli studenti ha già osservato, vale a dire che un lato della piastrella è doppio (o la metà dell'altro ).
- Un errore è considerare che il rapporto tra le due dimensioni del rettangolo sia 2, come quello di ogni lastra; che porta alle dimensioni 5 e 10 unità (invece di 6 e 9) poi 2,5 e 5 (in metri), alla superficie di 12,5 mq e al prezzo di 375 euro. Questa è una confusione tra la misurazione dell'area e quella del perimetro.
L’analisi a posteriore di elaborati delle sezioni di Riva del Garda, Rozzano, Sassari e Toscana Nord ha evidenziano una varietà molto ampia di procedimenti che portano alla risposta corretta a seconda delle diverse "visioni" della piastrellatura: un grande rettangolo le cui dimensioni sono 6 e 9 unità, le 27 tessere rettangolari (1 x 2), i 54 quadrati della griglia, tre allineamenti orizzontali - che danno luogo a successioni diverse delle tre operazioni: trasformazione delle unità in m o m2, calcolo delle superfici, calcolo del prezzo. Ad esempio contare i 54 quadrati, trovare le due dimensioni del pavimento 6 e 9, passare alle misure in metri per determinare l'area di un quadrato con lato di 0,5 m poi quella dell'area del pavimento, per finire con il calcolo del prezzo.
Tuttavia, ci sono conoscenze più basilari da osservare che riguardano le relazioni tra perimetro e area. Una pavimentazione di 15 metri di perimetro potrebbe dare aree diverse a seconda della disposizione delle mattonelle che la compongono. Scegliendo una pavimentazione a griglia (tutte le mattonelle del pavimento sono quadrate) con un perimetro di 15 metri, possiamo chiederci quali potrebbero essere le aree di questa pavimentazione, dalla più piccola alla più grande.
Più in generale possiamo passare ad un rettangolo senza griglia, e chiederci, per un dato perimetro, quale potrebbe essere l'area del rettangolo. Questo è un problema essenziale da risolvere con misurazioni che non siano più numeri di... (aree o lati dei quadrati) ma numeri reali. Ci avviciniamo così al passaggio dalle quantità discrete alle quantità continue, dai numeri interi ai numeri reali.
Disponiamo di quattro versioni dello stesso problema, con valori diversi delle variabili didattiche, i cui risultati nelle prove, danno indicazioni di interesse per determinate categorie
Il pavimento di Fabio pavimentazione con perimetro di 15 m composto da 27 rettangoli di (1 ⋅ 2); accessibile in catégorie 8 et vraisemblablement en cat. 7, voire 6.
La scatola (11.F.09, cat 5-7), pavimentazione con perimetro di 112 cm, composto da 4 rettangoli di (1 x 3); accessibile alla cat. 6 e risolto bene in cat. 7.
Pavimento di legno (23.I.14, cat 7-10) pavimentazione con perimetro di 15 m composto da 50 rettangoli di de (1 x 3); troppo difficile in cat.7 , accessibile dalla cat. 8.
Il tavolo da giardino (15.I.12, cat 6-7) pavimentazione composta da 7 rettangoli di (1 x 5), ciascuno con perimetro di 3 m, difficile in cat. 6 e accessibile in cat. 7
Questi dati sono utili per la scelta di un percorso didattico: alcune versioni possono essere utilizzate dopo un periodo piuttosto lungo.
Altri problemi che possono essere integrati in un percorso sul tema “area e perimetro” sono proposti dal gruppo di lavoro “Geometria piana”, alcuni dei quali sono attualmente (2023-2024) in fase di sperimentazione:
Particolarmente :
La torta di Nonna Lucia (22.II.06, cat. 4-6) dove la suddivisione di un rettangolo tramite le sue diagonali evidenzia dei triangoli le cui dimensioni (e i perimetri) sono evidentemente differenti, ma le aree sono uguali.
Le superfici del signor Barattolo (16.II.06, cat. 4-5) dove la quadrettatura permette di confrontare aree di rettangoli e di un poligono con otto lati.
L'eredità (08.I.16, cat. 7-8) (Gazzetta n. 4) dove ritroviamo la suddivisione di un rettangolo in due coppie di triangoli di dimensioni differenti, ma con aree equivalenti.
I sette poligoni (29.I.13, cat. 7-8) completo come analisi a posteriori 29.I. (Gazzetta n. 12)
Taglia e ritaglia (15.I.10, cat.5-6) per rinforzare il concetto di unità comune.
Tre amici e i loro disegni (20.II.06, cat.4-6) sul "conflitt"o area-perimetro.
Il tangram del falegname (I) (29.II.10, cat.6-7) et Il tangram del falegname (II) (29.II.17, cat.8-10) dove le relazioni tra i sette pezzi del tangram fanno intervenire le unità comuni delle aree e dei perimetri.
Spirale di quadrati (I) (23.II.11, cat, 6-8) et Spirale di quadrati (II) (23.II.19, cat, 9-10) con due notevoli sequenze corrispondenti: la progressione aritmetica dei lati di ragione √2 e la progressione geometrica delle aree di ragione 2!
Oltre alla risoluzione di questi problemi, la ricerca sistematica può essere proposta come rinforzo e lavoro a lungo termine:
- lo studio di una famiglia di triangoli dello stesso perimetro, ...
- lo studio di una famiglia di rettangoli della stessa area, ...
Articolo in preparazione sulla Gazetta no 14 : Percorsi didattici per la geometria piana con problemi del RMT Gruppo Geometria per i grandi
(c) ARMT, 2017-2024