
Banca di problemi del RMT
gp121-it
 |
Banca di problemi del RMTgp121-it |
|
Riconoscere i triangoli formati dai lati e dalle diagonali di trapezi le cui misure delle basi (8 e 12) e dell’altezza (15) sono date, calcolare le loro aree e constatare che sono indipendenti dalla misura degli angoli del trapezio.
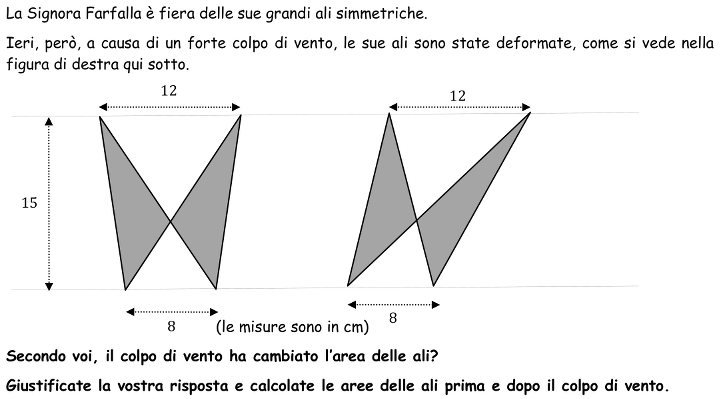
- Per ciascuna delle due figure, osservare che i triangoli formati da un’ala grigia e da un triangolo bianco piccolo hanno una base di 8 cm e l’altezza corrispondente di 15 cm, quindi hanno la stessa area. Dedurne che in ciascuna figura, le due ali grigie hanno la stessa area. Resta da confrontarle nel passaggio da una figura all’altra. Si può anche lavorare con il triangolo bianco grande.
Metodo sperimentale:
- Riprodurre su un foglio di carta quadrettato le due figure della farfalla e le due rette parallele esprimendo le misure date, 15, 12 e 8, in lati di quadretto. Rendersi conto sperimentalmente che, in ciascuna farfalla, le due ali si intersecano in un punto che dista 6 lati di quadretto dalla retta in basso e 9 dalla retta in alto.
- Verificare che tali valori sono corretti perché calcolando l’area delle due ali di una stessa farfalla si trova lo stesso valore (36 in quadretti), prima partendo dall’area del triangolo formato da un’ala e dal triangolo bianco piccolo e togliendo l’area di quest’ultimo, poi partendo dall’area del triangolo formato da un’ala e dal triangolo bianco grande e togliendo l’area di quest’ultimo. Dedurne che il colpo di vento non ha cambiato le aree delle ali.
Osservazione: le misure prese direttamente sulle figure nel testo non possono portare al calcolo dell’area delle ali, né alla conclusione che le aree dei triangoli grigi sono le stesse, a causa delle inevitabili approssimazioni.
Metodo algebrico per il calcolo dell’area di un’ala:
- Osservare che le ali della Signora Farfalla sono inscritte in due trapezi di basi 12 cm e 8 cm e di altezza 15 cm e quindi di stessa area (A = (12 + 8) × 15 / 2 = 150 cm2).
- Qualunque sia la figura considerata, indicare, per es., con a l’area di una delle due ali, con h l’altezza del triangolo piccolo, con H quella del triangolo bianco grande, e con A l’area del trapezio. Per le due figure, si hanno le relazioni: H + h = 15 ; A = 2a + 4h + 6H e a = 4×15 – 4h. Ricavare l’equazione in h : 8×15 – 8h + 4h + 6(15 – h) = 150, da cui h = 6.
- Per le due figure, l’area di un’ala è quindi uguale a 4 × 15 – 4 × 6 = 36 cm2. Il colpo di vento non ha cambiato le aree delle ali.
Metodo geometrico per il calcolo dell’area di un’ala:
- Dopo aver dimostrato che, per ogni farfalla, le due ali hanno la stessa area, lavorare sulla figura di sinistra e osservare che la diagonale AC (o analogamente la diagonale BD) divide il trapezio ABCD in due triangoli, ACB e ACD. Il triangolo ACB ha area 8 × 15 / 2 = 60 cm2 e il triangolo ACD ha area 12 × 15 / 2 = 90 cm2.
- Poiché ciascuno di questi triangoli è formato da un triangolo grigio e da uno bianco e i triangoli grigi sono equivalenti, la differenza tra le aree (30 cm2) è dovuta alla differenza tra le aree dei triangoli bianchi.
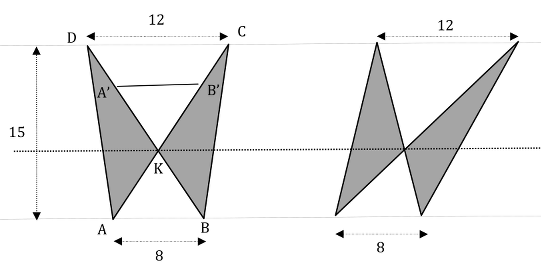
- Sia B’KA’ il triangolo simmetrico di AKB rispetto a K. L’area del trapezio A'B'CD è quindi uguale alla differenza delle aree dei triangoli AKB e DKC. L’altezza di questo trapezio è h = 30 × 2 / (12 + 8) = 3 cm. L’altezza del triangolo AKB è di conseguenza uguale a (15–3) / 2 = 6 cm e quella del triangolo DKC è uguale a 9 cm.
- Si può quindi calcolare l’area delle ali della farfalla (36 cm2 ciascuna), per esempio per differenza tra l’area del triangolo DAB (15 × 8/2) e quella del triangolo piccolo bianco KAB (6 × 8/2).
- Eventualmente considerare la retta passante per i centri delle ali, e ipotizzare intuitivamente che sia parallela alle altre due (si veda disegno più sopra).
- Comprendere allora che i triangoli bianchi piccoli nelle due figure hanno la stessa area, poiché hanno le basi della stessa lunghezza (8 cm) e la stessa altezza. Analogamente per i triangoli bianchi grandi. Poiché i triangoli formati da un’ala grigia e da un triangolo bianco piccolo hanno la stessa area, dedurre che le 4 ali disegnate nelle due figure hanno la stessa area e che il colpo di vento non ha modificato l’area delle ali della Signora Farfalla.
Oppure (soluzioni esperte):
- Osservare che nella figura a sinistra come in quella a destra, i due triangoli bianchi sono simili (angoli corrispondenti uguali) o omotetici (il centro di omotetia è il vertice comune dei triangoli grigi) il cui rapporto è uguale a quello delle loro basi (che sono delle stesse lunghezze nelle due figure): 8/12 = 2/3. Le loro altezze sono pertanto anch'esse nello stesso rapporto, 2/3. La distanza tra le due basi, 15 cm, è la somma dell'altezza del triangolo bianco grande e di quella del triangolo bianco piccolo, che è i 2/3 di quella del grande, cioè 1 + 2/3 = 5/3 dell'altezza del triangolo bianco grande. Si possono così dedurre le due altezze dei triangoli bianchi: quella del grande 15 : 5/3 = 9 cm e quella del piccolo 15 : 5/2 = 6 cm.
Oppure:
- Per il teorema di Talete, ponendo x = altezza del triangolo bianco piccolo e 15 – x = altezza del triangolo bianco grande, si ottiene l’equazione: (15 – x)/x = 12/8 per trovare x = 6 cm.
- Le aree dei triangoli bianchi sono dunque, per il grande: (12 × 9)/2 = 54 (in cm2) e per il piccolo (8 × 6)/2 = 24 (in cm2).
- Infine, calcolare l’area dei triangoli grigi, che è la stessa nella figura simmetrica come nell’altra, per ciascuna delle quattro ali della figura. Per esempio, partendo dal triangolo formato dal triangolo bianco piccolo e da un triangolo grigio, si trova: (8 × 15 /2) – 24 = 36 (in cm2).
Punteggi attribuiti su 1164 classi di 19 sezioni:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 8 | 509 (64%) | 123 (16%) | 136 (17%) | 15 (2%) | 9 (1%) | 792 | 0.6 |
| Cat 9 | 114 (58%) | 38 (19%) | 32 (16%) | 9 (5%) | 4 (2%) | 197 | 0.74 |
| Cat 10 | 102 (58%) | 32 (18%) | 31 (18%) | 4 (2%) | 6 (3%) | 175 | 0.74 |
| Totale | 725 (62%) | 193 (17%) | 199 (17%) | 28 (2%) | 19 (2%) | 1164 | 0.65 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
Secondo i criteri dell’analisi a priori:
La riuscita media molto bassa, di 0,65, di questo problema, ha posto numerosi interrogativi al Gruppo Geometria piana sia sulla gestione da parte degli allievi degli aspetti geometrici del problema e sia sui criteri di attribuzione dei punteggi che potrebbero aver indotto molti correttori a non attribuire almeno 1 punto laddove ci fosse un inizio corretto di ragionamento. La media dei punteggi non dà peraltro conto di alcune differenze significative da sezione a sezione.
Dall’analisi a posteriori si evince una difficoltà, da parte di alcuni correttori, ad interpretare le procedure degli allievi, espresse spesso con un linguaggio non formale, all’atto della correzione degli elaborati della prova e ad attribuire il punteggio “0”, anche laddove sia presente un inizio di ragionamento corretto, come, ad esempio, la ricerca e il calcolo delle aree dei trapezi. Purtroppo questo aspetto non è stato segnalato nei criteri per il punteggio “1” come è, peraltro, da tradizione.
Per quanto riguarda il punteggio “0”, più che di vera incomprensione, l’analisi a posteriori sembra mostrare che si tratti di “errata o insufficiente gestione” del problema stesso.
E’ spesso mancata la necessità di una giustificazione che i triangoli bianchi abbiano la medesima altezza e che tale giustificazione esige il calcolo dell’altezza.
In effetti le strategie indicate nell’analisi a priori si sono rilevate, per la parte formale, troppo elevate e anche nel caso di elaborati risolti correttamente, la via seguita è stata di tipo sperimentale che si è appoggiata per quanto riguarda l’altezza dei triangoli, sul disegno.

Problemi come quello in oggetto, ripresi in classe potrebbero mettere gli allievi in situazioni di ricerca e la successiva discussione per mettere a confronto le soluzioni di ciascuno, potrebbe aprire una strada verso aspetti deduttivi che portino a considerazioni generali.
Potrebbe essere avviata, tramite il problema “La signora farfalla”, un’attività ricca di aspetti geometrici con anche l’uso di un linguaggio algebrico, tra essi interconnessi.
Ad esempio, il teorema di Talete potrebbe trovare un’interessante collocazione del tipo: ponendo x = altezza del triangolo bianco piccolo e 15 – x = altezza del triangolo bianco grande, si ottiene l’equazione: (15 – x)/x = 12/8 per trovare x = 6 cm. Le aree dei triangoli bianchi sono dunque, per il grande: (12 × 9)/2 = 54 (in cm2) e per il piccolo (8 × 6)/2 = 24 (in cm2). Resta infine, da calcolare l’area dei triangoli grigi, che è la stessa nella figura simmetrica come nell’altra, per ciascuna delle quattro ali della figura. Per esempio, partendo dal triangolo formato dal triangolo bianco piccolo e da un triangolo grigio, si trova: (8 × 15 /2) – 24 = 36 (in cm2).
Da un punto di vista prettamente intuitivo, la maggior parte degli elaborati analizzati riporta la risposta “no, il colpo di vento non ha cambiato l’area delle ali”. E proprio a partire da tale intuizione in classe si potrebbe avviare una discussione sulla necessità di “provare” tale intuizione. Di passare cioè da “è evidente”, tanto spesso evocato di fronte a figure geometriche, a “ora è certo che sia così”, per chiunque.
(c) ARMT, 2017-2024