Il campo raddoppiato

Identificazione

Rally: 26.I.09 ; categorie: 5, 6, 7 ; ambito: GP
Famiglie:

• CA - Confrontare aree
• COG - Effettuare una costruzione geometrica
• QUA - Lavorare su una quadrettatura
• QUA/GQ - Gestire poligoni su carta quadrettata

Remarque et suggestion

Sunto

Trasformare un poligono concavo (formato da un rettangolo e da un quadrato o da tre quarti di un quadrato) sul contorno del quale sono fissati cinque punti, in un rettangolo di area doppia, che mantenga sul proprio contorno i cinque punti nella posizione originaria.

Enunciato

Compito per la risoluzione e saperi mobilizzati

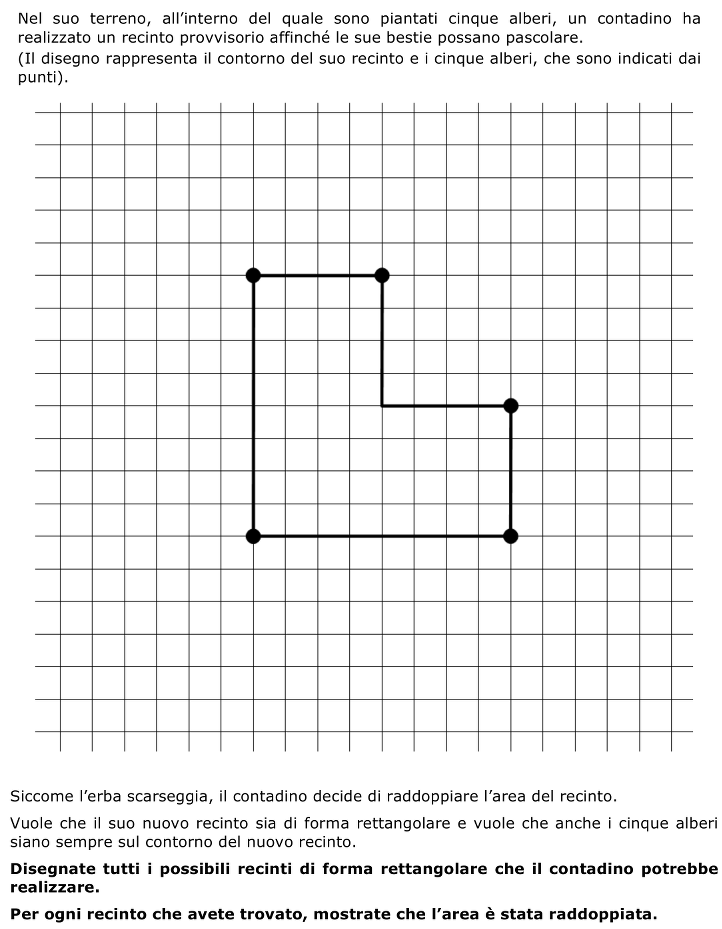
- Comprendere che la superficie racchiusa dalla nuova recinzione deve essere il doppio di quella precedente.

- Fare una scelta di un’unità di misura, la cosa più semplice sarebbe di prendere per unità un quadretto della quadrettatura e determinare l’area, in quadretti, della prima superficie (48) e quella della seconda (96)

Si può anche osservare che la figura di origine è composta da 3 quadrati di 4 x 4 e che il nuovo recinto dovrà essere composto da 6 quadrati di 4 x 4, ciò che permette di ottenere facilmente le due prime soluzioni (per il terzo si dovrà scomporre questo quadrato in triangoli la cui area vale ½ o ¼ del quadrato)

- Capire il vincolo della posizione dei cinque alberi: restano lì dove sono e devono anche essere sulla nuova recinzione. Poiché gli alberi sono cinque, non possono essere tutti sui vertici del rettangolo (come erano sui vertici della figura d’origine), ma quindi su dei lati del rettangolo.

- Provare a tracciare la nuova recinzione tenendo conto dei tre vincoli: deve essere rettangolare e i punti devono essere sui lati o essere i vertici del rettangolo.

Si presentano due casi:

• i lati del rettangolo seguono i lati della quadrettatura. Utilizzare allora il vincolo sull’area, 96, per determinare le dimensioni del rettangolo (si impongono rapidamente 8 e 12 come divisori di 96 e 8 come una delle dimensioni della figura di origine).
• i lati del rettangolo non seguono le linee della quadrettatura. Procedere per tentativi per tracciare il solo rettangolo che soddisfi il vincolo sulla posizione dei punti. Determinare la sua area e confrontarla con l’area del vecchio campo o confrontarla a quella della figura precedente per scomposizione.

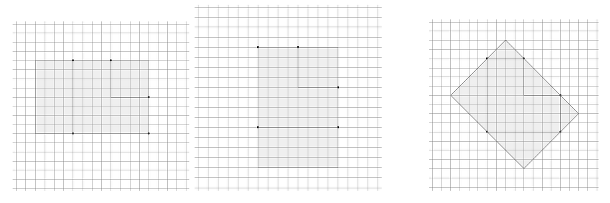
- Concludere che ci sono tre possibilità:

Risultati

26.I.09

Punteggi attribuiti su 3351 classi di 18 sezioni:

Secondo i criteri dell’analisi a priori:

• 4 punti: Risposta corretta con disegno preciso dei tre rettangoli possibili e verifica del raddoppiamento dell’area, senza alcuna figura errata
• 3 punti: Disegno chiaro dei tre rettangoli corretti senza verifica del raddoppiamento dell’area
  oppure disegno chiaro di due dei possibili rettangoli con verifica del raddoppiamento dell’area senza nessuna figura errata
  oppure disegno chiaro dei tre rettangoli corretti con o senza verifica del raddoppiamento dell’area e con la presenza di una figura errata (sia perché la figura non è un rettangolo, sia per eventuali alberi non sul confine)
• 2 punti: Disegno chiaro di uno solo dei possibili rettangoli, con o senza verifica del raddoppiamento dell’area, senza nessuna figura errata
  oppure due rettangoli corretti, con o senza verifica del raddoppiamento dell’area, con la presenza anche di una figura errata
• 1 punto: Disegno chiaro di uno solo dei possibili rettangoli, con o senza verifica del raddoppiamento dell’area, con la presenza di una figura errata
• 0 punto: Incomprensione del problema

(c) ARMT, 2018-2024