La pont des amoureux

Identification

Rallye: 26.II.13 ; catégories: 8, 9, 10 ; domaine: GP
Famille:

• TR - Construire, utiliser et/ou effectuer une transformation géométrique

Envoyer une remarque ou une suggestion

Résumé

Déterminer une ligne polygonale dont la longueur est la plus courte possible, incluant un segment le plus court possible entre deux parallèles, dans le contexte d’une rivière à traverser.

Enoncé

Tâche de résolution et savoirs mobilisés

Analyse de la tâche a priori

- Comprendre que le pont, pour être le plus court possible, doit être perpendiculaire aux berges de la rivière (distance entre deux droites parallèles).

- Essayer d’abord différentes positions du pont, en reliant les extrémités du pont aux maisons, et en comparant les longueurs des trajets obtenus.

- Se rendre compte que les écarts entre les longueurs obtenues lors des différents essais sont petits et que des mesures ne seront pas suffisantes pour répondre avec précision à la question posée.

- Réaliser que la longueur du pont est constante puisque les berges sont parallèles et qu’elle n’a pas d’influence sur la longueur d’un trajet.

- Donc chercher le chemin le plus court revient à chercher la position du pont [CD] tel que la distance JC+DR soit minimale. Le plus important est de bien placer le point C pour tracer le plus court chemin allant d’une maison à l’autre.

- Pour cela, procéder par exemple de la manière suivante : placer un point R’ tel que CDRR’ soit un parallélogramme :

1. Prendre la distance entre les berges : tracer une perpendiculaire aux berges et prendre la distance entre les points d’intersection de cette droite avec les droites représentant les berges
2. À partir du point R, tracer un segment RR’ perpendiculaire aux berges de longueur égale à l’écartement entre les berges

- Comprendre que rechercher la distance JC+DR minimale revient à rechercher la distance JC+CR’ minimale, car CR’ est égal DR puisque CDRR’ est un parallélogramme.

- Prendre conscience que cette distance est minimale si le point C est aligné avec J et R’ puisque J et R’ sont fixés par l’énoncé ou les constructions qui en découlent.

- Tracer la droite (JR’) et placer le point C, point d’intersection de (JR’) avec la berge la plus proche de J

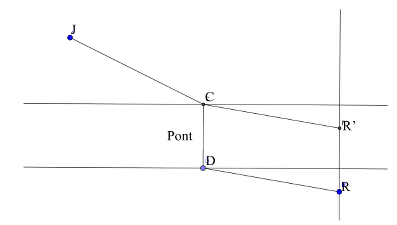
- Tracer le chemin suivant :

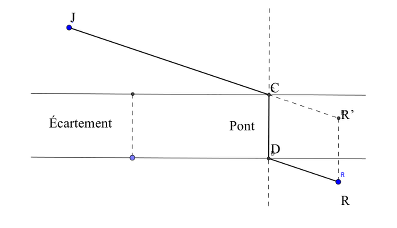
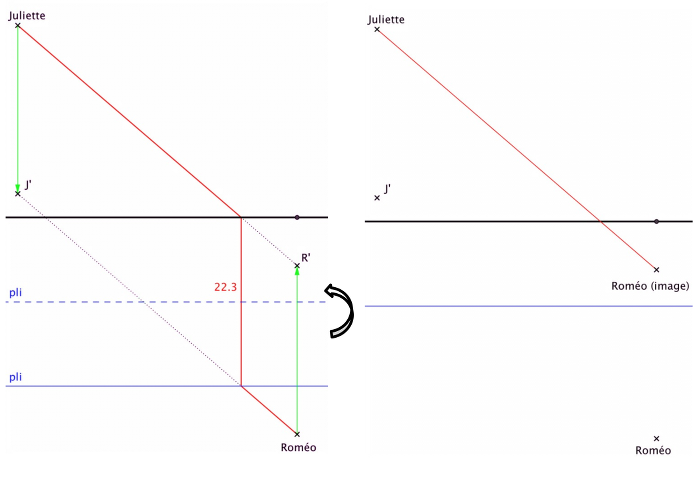
Ou, effectuer le même raisonnement en construisant le point J’ tel que JCDJ’ soit un parallélogramme ; puis, en traçant J’R, on obtient le point D, intersection de (J’R) avec la berge la plus proche de R. Ou, effectuer une translation du point J (ou du point R) correspondant à la distance entre les berges, par construction ou par double pliage (voir schéma ci-dessous), afin de faire abstraction de la rivière et de ne prendre en compte que la partie « route » du trajet.

- Tracer le segment RJ’ (ou JR’) de manière à trouver à l’intersection l’une des deux extrémités du pont. Tracer enfin le pont demandé.

Notions mathématiques

géométrie plane, droites parallèles, ligne brisée, longueur, minimum

Résultats

26.II.13

Points attribués, sur 1178 classes de 18 sections:

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Solution correcte avec construction d’un parallélogramme ou présence d’une translation (par construction ou par pliage) permettant de faire abstraction de la rivière, avec démarche détaillée, faisant apparaître la notion de distance minimale entre deux points et entre deux droites et montrant que le chemin construit est le plus court.
• 3 points: Solution correcte sans explication ou avec explication peu claire ou incomplète.
• 2 points: Présence d’au moins 4 essais avec pont perpendiculaire. Comparaisons des longueurs et choix d’une réponse cohérente avec les essais.
• 1 point: Tracé d’une route erronée, mais avec un pont perpendiculaire aux berges.
• 0 point: Incompréhension du problème (par exemple tracé de la route avec un pont non perpendiculaire aux berges).