
Banque de problèmes du RMT
gp135-fr
 |
Banque de problèmes du RMTgp135-fr |
|
Envoyer une remarque ou une suggestion
Diviser un triangle en trois triangles d’aires égales par deux segments : le premier issu d’un sommet dont l’autre extrémité se situe sur le côté opposé, le second issu de ce dernier point et dont l’autre extrémité se situe sur un autre côté. Indiquer la position de ces deux points sur les deux côtés, de 24 cm et de 18 cm de longueur.
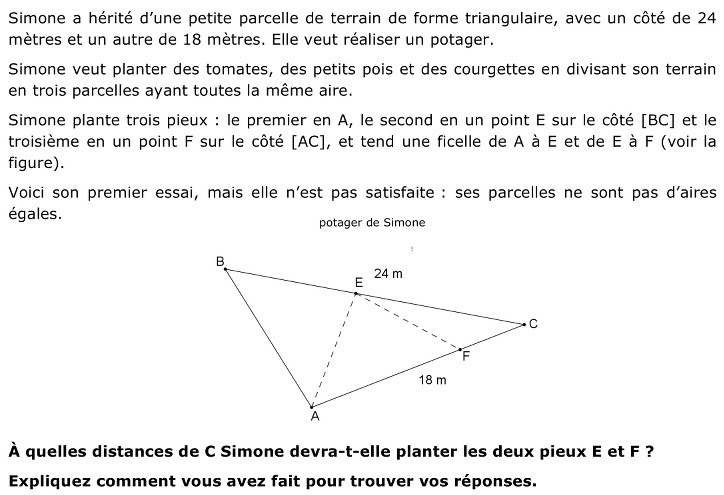
Appropriation
Observer les trois triangles qui doivent être équivalent selon l'énoncé et comparer leur position dans le triangle entier ABC, (indéterminé car seulement deux deux côtés sont donnés : 24 m et 18 m):
- le côté EB du triangle de gauche, ABE, est sur le côté BC de ABC. Ces deux triangles ont la même "hauteur" issue du sommet A.
- les côtés AF et FC des triangles du centre, AEF et de droite, FEC sont sur le côté AC du grand triangle. Ces trois triangles ont la même "hauteur" issue du sommet E.
Savoirs mobilisés
Formule de l'aire du triangle et proportionnalité entre les "bases" et les aires de triangle de même hauteur, ce qui se traduit pour le triangle de gauche et le grand triangle par "la mesure de la base du premier est le tiers de la mesure de la base du second"; et pour les deux triangles de droite, de sommet E: "les deux bases sont de même longueur"
Procédures
Par calcul mental, E se situe à 8 m de B et à 16 m de C; F se situe à 9 m de A et de C.
Si ce "savoir" sur la proportionnalité entre l'aire et la base ou entre l'aire et la hauteur d'un triangle n'est pas perçu et par conséquent pas "mobilisable", il est possible d'arriver à la solution par le dessin d'un cas particulier de triangle dont deux côtés mesurent 24 et 18 (unités de longueur), et d'effectuer les calculs à partir de mesures prises sur sa hauteur ou par algèbre ou de retrouver les bases à partir de l'égalité des aires, selon la formule.
géométrie plane, figure, triangle, segment, base, hauteur, aire, formule, proportionnalité, partage, double,
Points attribués, sur 396 classes de 8 sections:
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 9 | 180 (89%) | 10 (5%) | 6 (3%) | 4 (2%) | 3 (1%) | 203 | 0.23 |
| Cat 10 | 163 (84%) | 11 (6%) | 7 (4%) | 3 (2%) | 9 (5%) | 193 | 0.36 |
| Total | 343 (87%) | 21 (5%) | 13 (3%) | 7 (2%) | 12 (3%) | 396 | 0.29 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
Les résultats ci-dessus sont clairs: une petite minorité de groupes d'élèves de catégories 9 et 10 arrivent à la solution, comme pour la version I du problème Le potager (I) (26.II.12). Les quelques groupes qui ont trouvé la réponse n'ont pas procédé par proportionnalité en remarquant immédiatement que le point E se trouve au tiers du côté BC et que le point F est au milieu du côté AC; ils ont eu besoin d'exprimer l'aire des triangles.
Exemple 1.
{{img 26rmtii_fr-15a |}}
//E doit se trouver à 16 m de C et F doit se trouver à 9 m de C.
Je divise BC en trois parties congruentes => 24 : 3 = 8 dont chaque partie est congruente à 8.m => BH ≈ HW ≈ WC ≈ 8 m. Je relie A avec H et A avec W. je trouve ainsi trois triangles équivalents entre eux. T1 = T2 = T3.
BH ≈ HW ≈ WC ≈ 8m selon l'affirmation précédente (base) - AT en commun (hauteur) => 2T1 = T2 + T3
Le côté BC mesure 10 cm, dessiné horizontalement (base), il est partagé en trois parties par deux points H et W. La hauteur TA est dessinée. L'écriture BH ≈ HW ≈ WC ≈ 8 m semble indiquer que les trois parties ne sont pas considérées comme égales (congruentes) mais comme des approximations. Pour la deuxième partie de la l'explication, un nouveau schéma est dessiné où les deux triangles T1 et T2 sont remplacés par T4 et T5.
{{img 26rmtii_fr-15b |}}
Exemple 2.
Procédure de résolution algébrique:
{{img 26rmtii_fr-15c |}}
L'échec presque total pour ce problème dans sa première version comme dans la seconde, remet en questions les objectifs de l'enseignement de la géométrie à l'école secondaire. D'autres problèmes comme Le manteau de Martin (17.F.14), Le terrain du père François (11.II.16), Le partage du rectangle (30.I.18), Des rectangles sur une planche à clous (I) (27.I.18), montrent que la proportionnalité entre l'aire d'un triangle et sa base n'est pas perçue par les élèves ou, plus généralement, la formule de l'aire du triangle n'est maîtrisée que dans le cas où la base et la hauteur sont données et qu'il s'agit de l'appliquer, comme un algorithme de calcul.
Une première réponse à la remise en questions serait de renoncer à ce type de problèmes en raison de l'indétermination du grand triangle, qui semble exiger une résolution algébrique. À partir de cette aire (24h/2), l'aire du triangle de gauche (BAE), qui en est le tiers, permet de poser l'équation (1/3)(24h/2) = bh/2 dont la solution est b = (1/3)(24h/2)/(h/2) qui peut, après simplification par h/2 aboutir à b = 24/3 = 8. Les expressions algébriques qui contiennent l'inconnue b et la grandeur indéterminée h seraient trop complexes pour percevoir la simplification !
Une deuxième réponse est de se référer à la proportionnalité entre les deux grandeurs: l'aire des triangles de même hauteur et la mesure de leurs bases, sont liées par une relation de type multiplicatif (même rapport, qui est en l'occurence la moitié de la mesure de la hauteur commune). Une des propriétés de cette relation de proportionnalité est bien connue et familière: si l'on double, si l'on triple, si l'on prend la moitié ou le tiers d'une des deux grandeurs ..., l'autre double ou triple ou est divisée par 2 ou par 3 ... . Selon cette conception, le rapport de proportionnalité, indéterminé et qui "disparaît" par "simplification" dans la résolution algébrique, n'intervient pas dans les calculs. Il suffit d'un tableau de valeurs de deux lignes (ou deux colonnes).
C'est ici qu'intervient la remise en question de l'enseignement de la géométrie et l'analyse des obstacles que rencontrent les élèves.
- Il faut peut-être remonter à la détermination de l'aire du triangle et, précédemment de celle du rectangle. (Voir le problème Les neuf rectangles (31.I.19)) pour expliquer l'un des obstacles qui apparaît dans Le potager. L'aire du rectangle est abordée à l'école primaire, sur des modèles où les mesures sont des nombres naturels, comme additions répétées de carreaux entiers, sans distinguer les mesures de segments (de l'espace à une dimension) de celles des aires (les carreaux, unités de mesure de l'espace à deux dimensions). Il paraît prématuré à ces niveaux de parler de proportionnalité et de ses propriétés. Ce n'est que plus tard que l'opération d'addition répétée devient une nouvelle opération, la multiplication, qui ne prend du sens que lorsqu'on quitte les nombres naturels pour passer aux décimaux puis aux rationnels.
- Un autre obstacle dont l'origine est bien connue: beaucoup d'élèves pensent ou croient que le triangle a une seule base et une seule hauteur et que la première est horizontale sur la figure et l'autre verticale, à l'intérieur du triangle. D'où vient cette croyance et sa persistance sur de nombreuses années ?
- Les formules d'aire ou de périmètre sont des expressions algébriques. Est-il vraiment indispensable de les aborder avant de passer à l'algèbre? Ne serait-il pas plus efficace d'aborder l'aire du rectangle (et du carré) comme le produit de deux côtés (à une dimension) perpendiculaires, puis celle du parallélogramme en référence à celle du rectangle (sans parler de base di de hauteur) puis de considérer le triangle comme un demi-parallélogramme, ... et de proposer des activités qui ne sont pas des applications de formules mais de découvertes de relations ente figures qui ont des liens de parenté ?
Les exploitations didactiques de ce problème du potager ne consisteraient-elles pas à abandonner l'aspect formel de l'enseignement de la géométrie et de s'attaquer aux obstacles qu'il a créés en l'absence de sens?