Un quarto segmento e molti triangoli

Identificazione

Rally: 26.F.15 ; categorie: 8, 9, 10 ; ambito: GP
Famiglie:

• IF - Identificare figure
• IF/INV - Fare un inventario
• IF/RC - Riconoscere e costruire figure elementari

Remarque et suggestion

Sunto

Cercare il maggior numero di triangoli che è possibile generare su una figura, tracciando un solo segmento in più e trovare un sistema per designarli.

Enunciato

Compito per la risoluzione e saperi mobilizzati

Analisi a priori

- Identificare i triangoli delle tre prime figure per capire che certi triangoli si sovrappongono parzialmente. La determinazione dei triangoli è immediata per le due prime figure. È meno immediata per i 5 triangoli della figura di Anna: 3 “elementari” e 2 composti da due regioni.

- Trovare qualche strategia che permetta di ottimizzare il numero di triangoli per il 4° segmento: cercare di dividere il maggior numero possibile di triangoli, posizionare una delle estremità su delle intersezioni già esistenti, …

- Trovare un metodo efficace per contare e designare i triangoli.

Per individuare tutti i triangoli, l'uso dei colori sarebbe molto difficile da gestire. Uno dei metodi più efficaci, che comunque esige un gran rigore, è designare le regioni della suddivisione con una lettera o con un numero e di stendere l’inventario dei triangoli formati da una regione, due regioni, tre regioni, …

È anche possibile attribuire una lettera ai punti di intersezione dei segmenti della figura e designare i triangoli con i loro tre vertici.

Si dà qui di seguito un esempio per designare le regioni della figura di Anna e tre esempi con delle disposizioni differenti del quarto segmento:

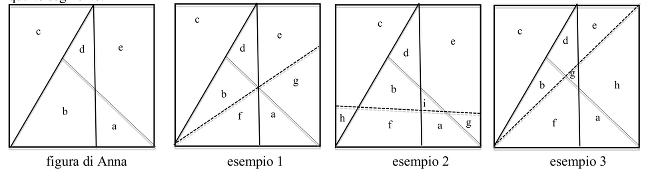
Esempio 1: il segmento divide le regioni b ed e in b, f, e, g. Vi si distinguono 11 triangoli, di cui 6 elementari: a, b, f, c, d; 2 composti da due regioni: a f - b d e 3 composti da tre regioni a b f - f a g, d b f.

Esempio 2: il segmento divide le regioni a, b e c. Vi si distinguono 10 triangoli, di cui 4 elementari: i, h, d, g; 4 composti da due regioni: a i - i b - c h - b d; 1 composto da tre regioni f b d; 1 composto da quattro regioni: a i f b.

Esempio 3: il segmento, diagonale del quadrato, divide le regioni b, d ed e. Vi si distinguono 15 triangoli, di cui 5 elementari: a, b, c, g, e; 5 composti da due regioni: a f - f g - b d – d g - g h; 2 composti da tre regioni: a f b - b d e; 3 composti da quattro regioni: f a g h - c b d e – f b g d.

Esistono altre disposizioni del 4° segmento che fanno comparire da 6 a 15 triangoli.

Nozioni matematiche

segment, triangle, dénombrement, identification, polygone, intersection, figure élémentaire

Risultati

26.F.15

Punti attribuiti, su 102 classi di 18 sezioni:

Secondo i criteri determinati nell’analisi a priori :

• 4 punti: Risposta: 15 triangoli, con disegno del segmento e individuazione chiara dei 15 triangoli
• 3 punti: Risposta: 13 o 14 triangoli, con disegno del segmento e individuazione chiara dei triangoli
  oppure risposta corretta, con disegno del segmento, individuazione confusa o assente dei 15 triangoli
  oppure il segmento tracciato corrisponde a 15 triangoli, ma manca la risposta 15 e solamente 13 o 14 triangoli sono indicati chiaramente
• 2 punti: Risposta: da 10 a 12 triangoli con disegno del segmento che li individua e individuazione chiara dei triangoli
• 1 punto: Risposta: da 7 a 9 triangoli con disegno del segmento che li individua e individuazione chiara dei triangoli
  oppure disegno del segmento e indicato solo il numero dei triangoli
• 0 punto: Incomprensione del problema o risposta con meno di 7 triangoli

(c) ARMT, 2018-2024