Triangoli sul geopiano

Identificazione

Rally: 27.I.18 ; categorie: 8, 9, 10 ; ambiti: GP, GM
Famiglie:

• CA - Confrontare aree
• CA/P - Confrontare aree su una quadrettatura
• LA - Utilizzare misure di lunghezze e aree
• LG - Determinare un luogo geometrico
• QUA - Lavorare su una quadrettatura
• QUA/GQ - Gestire poligoni su carta quadrettata

Remarque et suggestion

Sunto

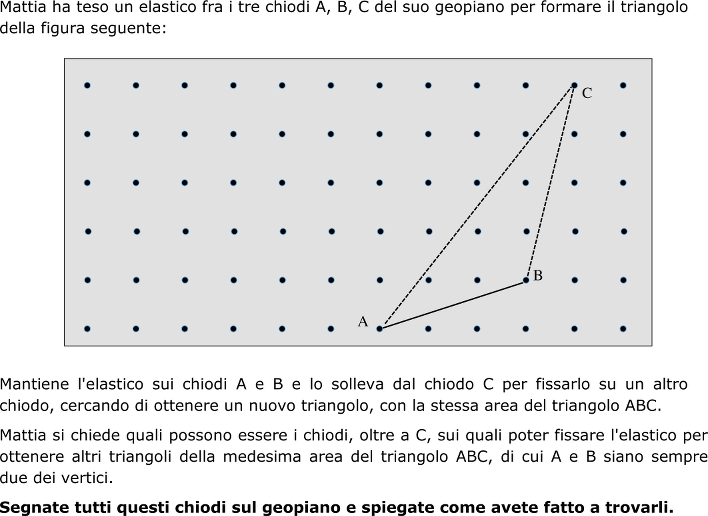
Un triangolo è determinato da tre vertici che si trovano sulle intersezioni di una griglia a maglia quadrata (geopiano); nessuno dei suoi lati è posizionato su una linea della quadrettatura. Trovare tutti gli altri triangoli della stessa area nei quali due vertici dati rimangono immutati e il terzo vertice è un altro nodo della griglia.

Enunciato

Compito per la risoluzione e saperi mobilizzati

Analisi a priori:

- Osservare la figura e comprendere che bisognerà tener conto dei limiti del geopiano, della disposizione dei chiodi su di esso e dell'elastico teso fra tre chiodi, della posizione obbligata dei due vertici e dell'area, che deve restare la stessa.

- Applicare la formula dell'area del triangolo come metà del prodotto delle misure di una base e dell'altezza corrispondente (bh / 2) e, per ragionamento deduttivo, arrivare alla conclusione che se la misura di un lato (b) e l'area (A) sono costanti, anche l'altezza (h) deve essere costante.

- Identificare l '"altezza" CH che é data dalla perpendicolare alla retta relativa alla base AB e rendersi conto che il punto H, intersezione delle due rette, non è sulla base ma sul suo prolungamento.

- Identificare la posizione in cui potrebbero essere posti i vertici diversi da C quando l'altra estremità H si sposta sulla retta AB; questi punti costituiscono il luogo geometrico dell’estremità del "segmento altezza", di misura costante che è la retta parallela alla base passante per C).

- Le tre constatazioni precedenti portano all'identificazione degli altri tre chiodi distinti da C situati sulla retta parallela ad AB passante per C.

Oppure:

- dopo aver capito che l'altezza del triangolo corrispondente al lato AB deve essere costante, si disegna e misura l'altezza CH, quindi si disegna la perpendicolare alla retta AB passante per un altro punto della griglia e su questa retta si misura la distanza dal punto alla retta AB. Se questa misura è uguale alla lunghezza CH, il punto è adatto, altrimenti si ricomincia con altri punti.

Oppure:

determinare l'area del triangolo ABC e cercare altri triangoli equivalenti che abbiano due vertici in A e B. Esistono diversi modi per determinare l'area, in particolare:

- l'area, 5,5 quadrati della griglia, si può calcolare con una “pavimentazione" (partendo da figure con aree facilmente determinate: rettangolo circoscritto, triangoli rettangoli), mediante scomposizioni e "sottrazioni" (un esempio è dato dalla figura qui sotto). La lunga e pesante procedura consiste quindi nell’esaminare altre posizioni del terzo vertice sulla griglia e nel determinare per pavimentazione l'area del triangolo così individuato. Il tentativo di spostare il vertice C di 1 quadrato a sinistra si tradurrebbe in un'area di 6; scendendo poi di 1 quadrato verso il basso, arriveremmo a 5, ecc.)

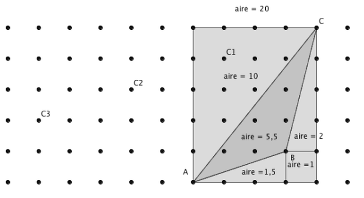
- Oppure determinazione approssimativa dell'area (per conteggio dei quadrati interi e unione di parti di quadrati o uso della formula dell'area di un triangolo partendo dalle misure, in cm, prese sulla figura).

Nota: l'area può essere calcolata con la formula di Pick (poiché c'è una griglia/geopiano A = p/2 + i - 1 = 3/2 + 5 - 1 = 5.5 (p indica il numero dei punti sui lati del poligono e i il numero dei punti all’interno del poligono)

Nozioni matematiche

triangolo, vertice, base, altezza, inventario, quadrettatura, perpendicolare, area. equivalenza, luogo geometrico, formula

Risultati

27.I.18

Punti attribuiti su 1254 classi di 20 sezioni:

Secondo i criteri determinati nell’analisi a priori :

• 4 punti: Risposta corretta con i tre punti (chiodi) C1, C2 e C3 (senza punti errati) e spiegazioni chiare (procedura tramite la parallela o altezza costante o calcolo delle tre aree, ...)
• 3 punti: Risposta corretta con i tre punti (chiodi) C1, C2 e C3 (senza punti errati) ma senza spiegazioni
  oppure dimenticanza di una o due posizioni, ma con una procedura corretta e ben spiegata (vedi spiegazione precedente)
  oppure trovati quattro punti "C" di cui tre corretti e la 4a posizione errata a causa di calcoli non sufficientemente precisi
• 2 punti: Una o due posizioni trovate ma senza spiegazione
  oppure calcolo corretto dell'area del triangolo ABC e almeno un tentativo di ricerca di altre possibili posizioni di "C" con calcoli di area dettagliati
• 1 punto: Calcolo dell'area del triangolo ABC mediante misurazioni
  oppure tentativo di determinazione dell'area del triangolo ABC senza arrivare al risultato corretto
  oppure altri inizi di ricerca coerenti ( per esempio affermazione che tutti i triangoli aventi la stessa base AB e la stessa area, devono avere la stessa altezza)
  oppure disegno del triangolo simmetrico del triangolo ABC rispetto all'asse del lato AB, questo triangolo ha la stessa area di ABC, ma il terzo vertice non è su un chiodo
• 0 punto: Incomprensione del problema

Procedure, ostacoli ed errori rilevati

Procedure

Sui 511 elaborati esaminati di categoria 8 e 244 delle categorie 9 e 10, delle sezioni BB, CA, FC, PR, PU, RZ, SI, SS, solo una parte delle classi ha trovato con procedura corretta almeno un chiodo con ragionamento corretto.

L’analisi a posteriori degli elaborati ha evidenziato che le procedure previste nell’analisi a priori sono state seguite da coloro che hanno risolto correttamente il problema. Nel complesso, la maggior parte degli alunni ha compreso il compito matematico, quello di costruire con un filo elastico altri triangoli equivalenti di quello dato; tuttavia, nella ricerca dei triangoli equivalenti, in molti elaborati, emergono diversi errori dovuti a misconcezioni relative al calcolo dell’area (formula errata) e al concetto di altezza di un triangolo. Anche quando la formula dell’area è corretta, la misura dell’altezza è presa su un segmento che è disegnato in posizione verticale, passante per il vertice C, ma non perpendicolare alla base AB, La misura di tale “altezza” viene espressa o in cm o in numero di chiodi. È emerso anche il misconcetto secondo il qual il “piede” dell’altezza si trova sempre nel punto medio della base.

In altri casi gli allievi sono andati alla ricerca di strategie non previste e in altri casi non adeguate alla risoluzione del problema.

Si è rilevata una differenza “cognitiva” tra gruppi che:

- risolvono con la procedura similare a quella dell’analisi a priori del tipo misura dell’altezza relativa ad AB, calcolo dell’area del triangolo e retta parallela e che utilizzano un linguaggio già ben strutturato, oppure con una procedura che mette in gioco l’altezza rispetto al lato AB e la sua successiva traslazione;

- gruppi che mostrano ancora confusione fra area e perimetro; - altri per i quali l’area di un triangolo si ottiene calcolando il semiprodotto fra due lati.

Tra questi “estremi”, oltre ai già citati gruppi che hanno trovato con procedura corretta almeno un chiodo corretto, ci sono stati diversi gruppi che non hanno trovato i chiodi corretti, ma che hanno comunque mostrato di essersi in qualche modo appropriati del problema, senza però rendersi conto che, ad esempio, utilizzare il ritaglio del triangolo dato o disegnare una sorta di simmetria assiale non soddisfaceva i due vincoli posti dal problema: stessa area e terzo vertice su un chiodo contemporaneamente.

In alcuni casi, gli alunni non sono riusciti a mantenere il controllo su tutte le condizioni poste dal problema e, nel tentativo di risolverlo, hanno proposto figure sbagliate perché, ad esempio, ottenute sollevando l’elastico da tutti i vertici, non solo da C, o perché non hanno compreso che il geopiano su cui individuare i triangoli equivalenti corrispondeva a quello raffigurato nel disegno.

Ostacoli ed errori

Il problema in oggetto ha permesso di far venire alla luce ostacoli ed errori riguardo a conoscenze e abilità a proposito di concetti che si pensa dovrebbero essere acquisiti nelle categorie alle quali è stato proposto.

Gli ostacoli principali evidenziati sono stati i seguenti:

1. La mancata identificazione dell’altezza relativa al lato AB in quanto gli allievi non si sono resi conto che il piede dell’altezza (H), intersezione delle due rette (base e altezza), non cade sulla base, ma sul suo prolungamento. In effetti, la definizione di altezza come: “segmento che parte da un vertice e cade perpendicolarmente sul lato opposto” potrebbe condurre gli allievi a considerare che l’altezza debba per forza di cose cadere sul lato, non riconoscendo perciò quelle che cadono sul suo prolungamento.

2. La mancata identificazione della posizione in cui potrebbero essere posti i vertici diversi da C quando l'altra estremità H si sposta sulla retta AB; questi punti costituiscono il luogo geometrico dell’estremità del "segmento altezza", di misura costante, che è la retta parallela alla base passante per C.

3. La non appropriazione del concetto di altezza, spesso considerata corrispondente ad uno dei lati del triangolo.

4. La difficoltà nel tracciare l’altezza, soprattutto quando le figure geometriche “non allineate” con l’orizzontale e la verticale e in particolare nel caso in cui l’altezza cada sul prolungamento del lato.

Gli errori principali emersi sono stati i seguenti:

1. Nel calcolo dell’area:

a. calcolo del semiprodotto della misura di due lati del triangolo;

b. calcolo del semiprodotto 4  5 /2 corrispondente ai lati del triangolo rettangolo la cui ipotenusa è AC e i cui lati sono orizzontali e verticali;

c. calcolo del semiprodotto della base e dell’altezza con misura errata di quest’ultima.

2. Disegno di una “sorta” di triangolo simmetrico del triangolo ABC facendo coincidere il vertice C1 con uno dei chiodi.

3. Applicazione errata della formula di Pick: gli allievi hanno considerato triangoli equivalenti quelli che avevano lo stesso numero di chiodi interni o lo stesso numero di quelli esterni.

Indicazioni didattiche

Questo problema, come altri del RMT ha messo ben in evidenza le difficoltà incontrate dagli allievi laddove hanno a che fare con le altezze di figure geometriche “non allineate” con l’orizzontale e la verticale (spesso poco prese in considerazione in manuali scolastici, benché non in tutti e che diventano figure “standard”) o in presenza di triangoli ottusangoli, o ancora laddove venga loro proposta solo la definizione di altezza come “segmento che parte da un vertice e cade perpendicolarmente sul lato opposto”. Da tali constatazioni scaturite dall’analisi anche di questo problema potrebbe essere utile:

1. Considerare come definizione di altezza di un triangolo “la distanza fra un lato, scelto come base, e il suo vertice opposto”.

2. Discriminare tra “altezza come segmento” o parte di retta e “altezza come misura”.

3. Superare la misconcezione dell’altezza intesa solo come verticalità.

4. Presentare figure geometriche rappresentate con orientazione diversa da quella orizzontale e verticale (B. Brogi, 2019).

5. Superare la misconcezione che il “piede” dell’altezza si trova sempre nel punto medio della base.

6. Riconoscere altezze in figure in cui il piede dell’altezza si trova sulla retta a cui appartiene la base.

7. Sviluppare il concetto di luogo geometrico determinato dalla traslazione dell’estremità del segmento altezza (di misura costante) quando questa si sposta su una retta. Ciò consentirà di acquisire che triangoli che hanno la stessa base e la stessa altezza sono equivalenti.

8. Proporre problemi in cui l’altezza non viene esplicitata, tratti ad esempio dalla Banca dei problemi dell’ARMT.

9. Progettare percorsi d’apprendimento utilizzando problemi tratti dalla Banca dell’ARMT, limitando il ricorso agli esercizi ripetitivi di calcolo delle aree presenti nei libri di testo.

Il problema Il ritaglio di triangoli (19.II.13 cat. 6,7,8) può concorrere ad abituare gli allievi a svincolarsi dal disegnare triangoli in posizione standard. La risoluzione di questo problema condurrà all’osservazione di quelle che con Raymond Duval (preprint, 2020) vengono indicate come “unità figurali 1D” che permetterà di individuare i lati di uguale lunghezza del triangolo isoscele come diagonale del rettangolo 4x2. Un problema come “Il ritaglio di triangoli” permette di far venire alla luce ostacoli caratteristici a proposito di nozioni che sembrerebbero acquisite, come il triangolo isoscele, la sua posizione e la congruenza di segmenti. Si osserva chiaramente che l’immagine di triangolo isoscele che hanno gli allievi è quella di una figura con tre lati di cui uno è orizzontale e gli altri due, congruenti, sono obliqui. Si tratta di una figura simmetrica con asse verticale (nel senso di Lismont & Rouche, 2001), dove l’oggetto di riferimento è “il tetto” (es. Marchini et al., 2002). Il termine "base" fa sì che quel lato non solo sia orizzontale ma anche "in basso". Il modello “bandiera”, (ancora nel già citato Marchini et al.), è molto meno frequente.

Nella Banca di problemi si trovano diversi problemi che affrontano problematiche discusse in precedenza. Fra gli altri:

Il Mantello di Martino (17.F.14 cat. 7, 8, 9, 10); La Signora Farfalla (25.II.16 cat. 8, 9, 10) ; L’Orto I ( 26.II.12 cat. 6, 7, 8)

Bibliografia

Brogi, B.: 2019, Matematica in classe con il Rally Matematico Transalpino, “un’insegnante racconta”/Mathématiques en classe avec le Rallye Mathématique Transalpin, « le témoignage d’une enseignante’, Gazzetta di Transalpino. 9, 117-123.

Duval, R.: preprint, Le premier seuil dans l’apprentissage de la géométrie : « VOIR » les « Figures »/Il primo passo nell’apprendimento: “VEDERE” le figure, Gazzetta di Transalpino n. 10 (apparirà sul sito dell’ARMT nel corso del 2020).

Lismont, L, Rouche, N. (a cura di), 2001, Forme et mouvements, CREM.

Marchini C., Rinaldi M.G., Bedulli M., Grugnetti L.: 2002, Tetti e bandiere, Processi didattici innovativi per la Matematica nella scuola dell'obbligo, Pitagora (Bo), 223-236.

(c) ARMT, 2019-2024