
Banca di problemi del RMT
gp145-it
 |
Banca di problemi del RMTgp145-it |
|
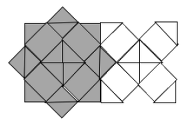
Calcolare il rapporto fra le aree di due tipi di figure di un mosaico, per scomposizione in quadrati, semiquadrati triangolari e rettangoli di cui un lato è quello di un quadrato e l’altro quello della sua diagonale.

- Immaginare la parte a partire dalla figura data e capire, vista la disposizione delle piastrelle, che il numero di quelle grigie e di quelle bianche è approssimativamente il medesimo su una parete costituita da migliaia di piastrelle e che è pertanto sufficiente calcolare l’area di una sola piastrella per colore per determinare il rapporto tra le parti in bianco e in grigio della parete.
- Osservare con attenzione i due poligoni, verificare che ciascuno abbia 16 lati disposti su una trama quadrata. Le piastrelle grigie occupano un quadrato della trama e quattro triangolini, “presi in prestito” dalle piastrelle bianche (si veda la figura 1). Osservare poi che le piastrelle grigie possono essere considerate come la sovrapposizione di due quadrati i cui lati rispettivi formano angoli di 45 gradi (o che si possa passare dall’uno all’altro con una rotazione di 45 gradi). Di conseguenza si può essere certi che tutti gli angoli acuti del poligono grigio sono retti.
- Passare all’analisi del contorno delle piastrelle e osservare che goni lato di un quadrato della trama è composto da due dei 16 lati del poligono, di 5 cm di lunghezza e da una diagonale di un triangolo rettangolo due lati del quale misurano 5 cm.
- A seguito di questa osservazioni, si può pensare alle aree delle piastrelle come quelle dell’area del quadrato della trama aggiungendovi o togliendo, rispettivamente per la piastrella grigia e per quella bianca, quelle dei quattro triangoli.
- Passare al calcolo delle aree delle due piastrelle:
en cm: diagonale di un triangolo, 5√2 o √50 ≅ 7,07; lato di un quadrato della trama: 10 + 5√2 ≅ 17,07
in cm2: area di quattro triangoli 4(25/2) = 50; area di un quadrato della trama (10 + 5√2)2 = 291,42… ≅ 290
area di una piastrella grigia o bianca (10 + 5√2)2 + 50 ≅ 340 oppure (10 + 5√2)2 - 50 ≅ 240
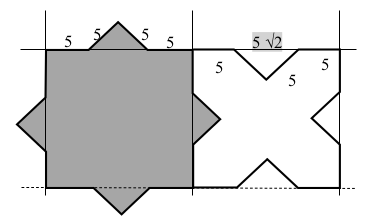
- Calcolare infine il rapporto delle aree in bianco e in grigio; cioè “area di una piastrella bianca”/”area di una piastrella grigia “: [(10 + 5√2)2 – 50 ]/ [(10 + 5√2)2 + 50] ≅ 240/340 ≅ 0,7 (La risposta esatta sarebbe √2/2 per coloro che sono capaci di effettuare le semplificazioni necessarie).
Oppure cercare di scomporre ciascuna piastrella con quadrati, rettangoli e triangolini ed effettuare i calcoli delle aree corrispondenti.
Ecco qualche esempio di queste piastrelle dove si tratta di riconoscere i lİati di lunghezza 5 e quelle di lunghezza 5√2 o √50. :
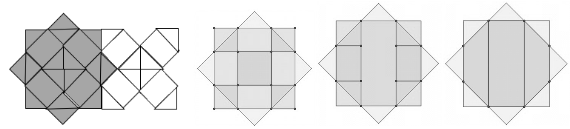
Nel primo esempio (figura 2) il quadrato grigio si scompone in 16 triangoli 8 rettangoli isosceli) e 4 rettangoli, il quadrato bianco in 8 triangoli e 4 rettangoli. Le aree dei triangoli misurano 12,5 = 25/2 cm2. I rettangoli hanno una larghezza di 5 cm, mentre la lunghezza è quella dell’ipotenusa di un triangolo che può essere calcolata con il teorema di Pitagora o come lato del quadrato centrale: √50 cm che possiamo arrotondare a 7,0 o 7,1. L’area di un rettangolo è pertanto 5 x √50 ≅ 35 ≅ 35,5.
area, poligono, misura, lunghezza, Pitagora, rapporto, pavimentazione, quadrato, triangolo, rettangolo, diagonale
Punteggi attribuiti su 1209 classi di 18 sezioni:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 8 | 436 (54%) | 201 (25%) | 79 (10%) | 44 (5%) | 49 (6%) | 809 | 0.85 |
| Cat 9 | 93 (45%) | 50 (24%) | 18 (9%) | 19 (9%) | 27 (13%) | 207 | 1.21 |
| Cat 10 | 63 (33%) | 41 (21%) | 28 (15%) | 24 (12%) | 37 (19%) | 193 | 1.64 |
| Totale | 592 (49%) | 292 (24%) | 125 (10%) | 87 (7%) | 113 (9%) | 1209 | 1.04 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
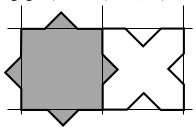
1.1 Percezione della trama delle piastrelle
Nella maggior parte dei casi il mosaico è percepito su una trama quadrata. Le piastrelle grigie occupano un quadrato della trama e quattro triangolini, presi in prestito dalle piastrelle bianche (si veda figura 3). Ogni lato di questo quadrato è composto da due dei 16 lati del poligono, la cui lunghezza misura 5 cm e dall’ipotenusa di un triangolo.
È allora sufficiente determinare la lunghezza dell’ipotenusa di un triangolino (√50 ≅ 7,07) poi il lato di un quadrato della griglia (10 + √50) ≅ 17,07 (en cm) per calcolare l’area di questo quadrato (10 + √50)2 ≅ 291,42 (in cm2).
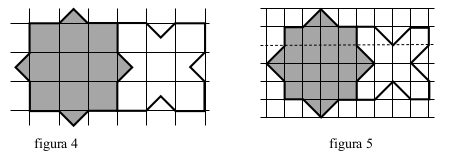
1.2. Gli errori di percezione dei “quadrati della griglia” o delle scomposizioni
Numerosi gruppi si fidano della loro percezione visiva dei contorni delle piastrelle o dei lati dei “quadrati della griglia” senza un’analisi “metrica” dei segmenti che li compongono. La maggioranza percepisce una suddivisione in 9 parti isometriche (3 x 3), (figura 4), altri in 16 parti (4 x 4) (figura 5). Nel caso della figura 4, il quadrato della griglia ha 15 cm di lato e la sua area è di 225 (in cm2). Un gruppo ha scelto 6 cm come parte centrale del lato del quadrato della griglia, facendo apparire dei triangoli isosceli considerati come semi-quadrati di lati 5 e 5 e 6 cm, di area 9 cm2.
1.3. Scomposizione in triangoli e rettangoli
Nei rari casi di scomposizione in 8 triangoli e 4 rettangoli per il quadrato bianco, 16 triangoli per il quadrato grigio, si trova il rapporto visivo errato “un rettangolo vale due triangoli” per arrivare, dopo la sostituzione, a 16 triangoli bianchi e 24 triangoli grigi e a un rapporto delle aree 16/24 = 2/3 O si arriva a contare 22 triangoli per la piastrella grigia e 14 per quella bianca. Si arriva poi al rapporto 7/11
2. Difficoltà nel calcolo di lunghezze e aree
In alcuni elaborati del tipo analizzato nel paragrafo 1.1, gli allievi arrivano a aree rispettive di ≅ 241 e ≅ 341 cm2 per le piastrelle bianche e grigie. Altri presentano confusioni, dimenticanze o errori nel calcolo della diagonale o dell’area dei triangoli piccoli.
Per esempio: area del quadrato bianco 241,42 area del grigio 291,42 (l’area dei 4 triangoli non è stata aggiunta per la piastrella).
Per quanto riguarda gli elaborati del tipo 1.2, una parte degli allievi arriva a aree rispettive di 175 e 275 cm2 per i quadrati bianchi e grigi, calcolati a partire da quella del quadrato 152 = 225. Gli altri presentano delle incoerenze; vi si trovano i 225 cm2 del quadrato della griglia, ma le aree dei quattro triangoli da aggiungere o togliere non appaiono. C’è infatti una difficoltà supplementare dovuta alla percezione erronea della griglia (3 x 3): le ipotenuse di 5 cm non si accordano con i lati di 5 cm degli altri lati. In un caso questi triangoli sono considerati come equilateri.
3. Difficoltà nel calcolo del rapporto
Le due aree delle piastrelle sono state trovate da alcuni gruppi correttamente (1.1) o con l’errore della percezione visiva (1.2); ma la risposta alla richiesta “Calcolate il rapporto tra le aree in bianco e le aree in grigio della parete.”, non è stata sempre corretta.
In alcuni casi il calcolo delle aree è stato esteso a quelle della ventina di piastrelle, complete o incomplete, della figura dell’enunciato, senza prestare attenzione alla “parte intera” né aver capito che è sufficiente confrontare le aree di una sola piastrella grigia con quella di una sola piastrella bianca.
Figurano anche diversi rapporti inversi o non giustificati.
Risposte molto parziali
In questi elaborati figurano tentativi di scomposizione delle piastrelle tutti differenti e incompleti, difficili da classificare.
Osservazioni
La media generale di «0,8» punteggi attribuiti può sembrare bassa, ma è necessario ricordare qui che la risposta del problema è la sintesi di tutti i compiti di risoluzione e bisogna pertanto interessarsi a ciascuno di essi piuttosto che a un compito “globale”.
Il primo compito menzionato della rubrica “Compito per la risoluzione e saperi mobilizzati”, laddove si limiti al confronto delle aree di una sola piastrella grigia e di una sola piastrella bianca, presenta una difficoltà per circa un terzo dei gruppi di allievi. Consideriamo questo compito come “evidente” e lo è per un adulto, ma non dobbiamo dimenticare che questo rapporto è solo un’approssimazione che dipende dal numero stimato di piastrelle intere della parete, nell’enunciato del problema tramite migliaia di piastrelle grigie e di piastrelle bianche.
Il secondo compito è quello di analizzare e scomporre le due piastrelle, confrontando le lunghezze dei segmenti della separazione (lati del poligono di 5 cm e altri lati dei triangoli, dei quadrati, dei rettangoli) indipendentemente dalle percezioni visive. È È qui che appare un ostacolo che dovremmo cercare di definire meglio.
Il terzo compito, è quello dei calcoli d’area con, prima, la determinazione della lunghezza dell’ipotenusa del triangolo rettangolo isoscele 5, ?, 5. La grande maggioranza dei gruppi che l’hanno a calcolata sono arrivati “7,07” con il teorema di Pitagora ma ci possiamo porre delle domande sulla natura della scrittura “7,07”. In alcuni casi è preceduta da √50, altre volte da √(25 + 25) o ancora da √(52 + 52 ), ma molto raramente seguito da un simbolo di approssimazione « ≅ ». In alcuni casi in cui questa diagonale ha permesso di determinare l’area del quadrato centrale della scomposizione (figure 6), il risultato è 7,072 = 49,98 al posto di 50.
L’applicazione del teorema di Pitagora sembra ancora di tipo algoritmico e si svolge in successione: 52 seguito da + 52 e da 52 + 52 prima di passare alla menzione della la √ . Non abbiamo trovato la scrittura 2 x 52 che potrebbe esprimere il fatto che l’area del quadrato costruito sull’ipotenusa è il doppio dell’area dei quadrati costruiti sui cateti; e neppure la scrittura 5√2. È a livello della categoria 10 che troviamo qualche caso di calcoli tutti con √2 compreso il rapporto.
Il quarto compito, del calcolo del rapporto, dipende evidentemente dalla riuscita nei calcoli che lo precedono. Le risposte differenti da quelle che si aspetta l’adulto sono verosimilmente dovute all’interpretazione del termine “rapporto” e dall’ordine delle due grandezze che lo determinano.
A proposito del triangolo rettangolo isoscele, la configurazione “particolare” del mosaico in oggetto ha condotto un certo numero di gruppi di allievi a “fidarsi” del primo colpo d’occhio e di conseguenza a non collegare ciò che vedevano nella figura alle proprietà del triangolo rettangolo isoscele, considerando che tutti i tre lati misurassero 5 cm.
In classe potrebbe essere interessante riprendere il problema, per esempio con un ingrandimento della figura, e avviare un dibattito proprio a proposito del triangolo, con riferimento al punto 1.2., descritto più sopra.
(c) ARMT, 2019-2024