La bergerie du berger Arthur

Identification

Rallye: 27.F.11 ; catégories: 6, 7, 8 ; domaine: GP
Familles:

• CA - Comparer des aires
• COG - Effectuer une construction géométrique
• QUA - Travailler sur un quadrillage
• QUA/GQ - Traiter des polygones sur quadrillages

Envoyer une remarque ou une suggestion

Résumé

Déterminer toutes les manières possibles de diviser, avec deux sortes de segments de longueurs données disposés parallèlement aux côtés, un rectangle en deux parties, dont l’un a une aire double de l’autre et chacune contenant un point donné.

Enoncé

Tâche de résolution et savoirs mobilisés

Analyse a priori:

- Comprendre que les barrières doivent être placées sur le quadrillage de la grille, parallèlement aux côtés du rectangle.

- Comprendre également, à partir de l'exemple, que toutes les barrières ne doivent pas nécessairement être utilisées à chaque fois.

- Calculer l’aire de l'enclos 96 m2 (12 × 8) et en déduire l'aire des deux parties : la plus petite 32 m2 (96 : 3) et la plus grande 64 m2 (2 × 32). Il est aussi possible de raisonner en prenant pour unité le carreau.

- Identifier la possibilité symétrique à celle donnée à titre d'exemple (fig.1).

- Comprendre qu’en utilisant uniquement des barrières de 4 mètres, il existe six autres possibilités pour réaliser la division interne de l'enclos en respectant les contraintes : avec deux barrières comme en fig.2 et fig.3 ; avec trois barrières fig.4 et fig.5, avec quatre barrières comme en fig.6 et en fig.7

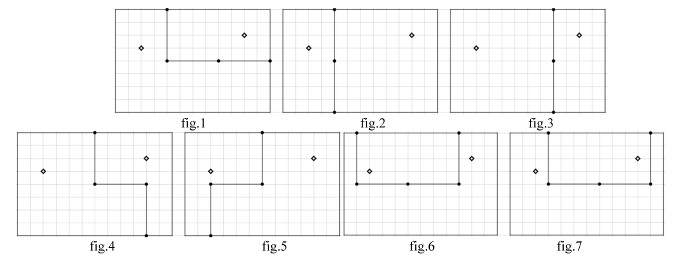
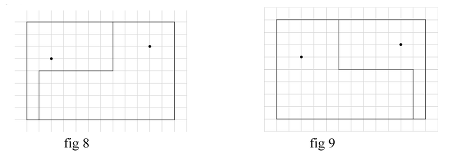
- De plus, en utilisant deux barrières de 4 mètres et celles de 6 mètres, on peut identifier deux autres possibilités (fig.8 et fig.9) :

Notions mathématiques

rectangle, aire, comparaison, quadrillage, périmètre

Résultats

27.F.11

Points attribués sur 244 classes de 21 sections:

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: 8 ou 9 figures correctes sans figures erronées.
• 3 points: 7 figures correctes sans figures erronées
  ou 8 ou 9 figures correctes avec au plus 2 figures erronées
• 2 points: 8 ou 9 figures correctes avec 3 figures erronées ou plus
  ou 7 figures correctes avec une ou plusieurs figures erronées
  ou 5 à 6 figures correctes avec ou sans figures erronées
  ou seulement 4 figures non symétriques identifiées, autres que celle donnée (par exemple fig. 2, 4, 6, 8)
• 1 point: Moins de 5 figures correctes, éventuellement avec quelques figures erronées
• 0 point: Incompréhension du problème