
Banca di problemi del RMT
gp16-it
 |
Banca di problemi del RMTgp16-it |
|
Confrontare le aree di due figure composte da triangoli e rettangoli i cui vertici sono tutti sulle intersezioni di una quadrettatura di base.
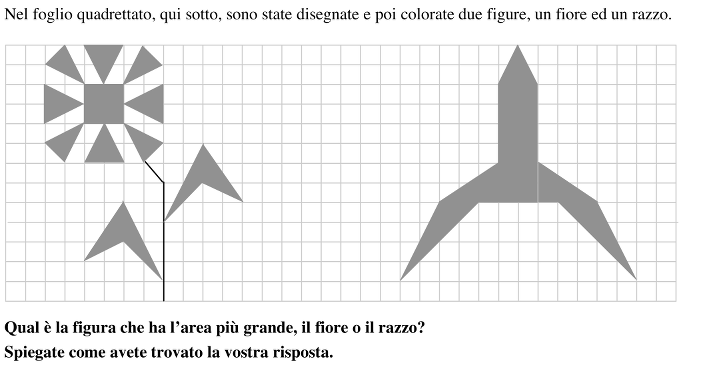
- Nel corso della fase di appropriazione del problema, sarà necessario rendersi conto che per rispondere alla domanda occorrerà determinare le misure di ciascuna area delle parti grigie perché le procedure per compensazione non permettono di andare al di là di quadrati e rettangoli. Il quadrato della quadrettatura si impone naturalmente come unità d’area (u), e che le procedure di conteggio o di ricoprimento sono inadeguate perché non si possono ricoprire i triangoli con quadrati interi.
Il compito per la determinazione delle aree si scompone in diverse fasi, per esempio:
- misurare le aree dei triangoli rettangoli considerandoli come metà di rettangoli (divisi in due da una diagonale). I due triangoli rettangoli del razzo sono dei semi rettangoli di 2 × 3 e hanno l’area che misura 3 u;
- decomporre i petali grandi del fiore e della punta del razzo in due triangoli rettangoli di 1 × 2 con area che misura 1 u. Si può anche vedere che questi due triangoli rettangoli occupano la metà del quadrato 2 × 2 nel quale sono inscritti e che la loro area misura 2 u;
- elaborare infine una strategia più complessa di decomposizione di un rettangolo nel quale è inscritto un triangolo grigio tenendo conto delle sue parti «bianche» da «sottrarre», che sono dei triangoli rettangoli. Esempio: ciascuna foglia del fiore può essere divisa in due parti, inscritte in rettangoli di 2 × 3 e 2 × 4, dai quali occorrerà eliminare dei triangoli rettangoli bianchi di 2 × 3 e 1 × 2, e, rispettivamente di 2 × 4 e 2 × 2, per arrivare a misure di area uguali a 2 u (6 – 3 – 1 et 8 – 4 – 2);
- calcolare le misure delle aree delle due figure per addizione. Per il fiore: : 4 + 4 × 2 + 4 × 1,5 + 4 × 2 = 26 (u) e per il razzo: 2 + 12 + 2 × 3 + 2 × 4 = 28 (u). Concludere che la parte grigia del razzo è più grande di quella del fiore.
Ci sono evidentemente numerosi modi di scomporre le figure o di ricomporle e poi di organizzare i calcoli. Il compito essenziale è di ottenere il risultato a partire da rettangoli interi o divisi in due. Bisogna saper scomporre le figure in triangoli rettangoli e determinare la loro aree per conteggio o calcolo dell’area di semi rettangoli. Per certe pari che non possono essere scomposte in triangoli rettangoli bisogna saperle inscrivere in rettangoli e lavorare per sottrazione di aree: quelle dei triangoli rettangoli complementari all’interno dei rettangoli circoscritti. La «formula» dell’area del triangolo qui non è utile in quanto le misure delle “basi” e “altezze” dei triangoli non rettangoli non possono essere determinate da parti intere dei lati della quadrettatura in quanto i triangoli non sono tutti in posizione tradizionale con la base orizzontale.
area, triangolo, rettangolo, scomposizione di una figura, poligono, quadrettatura, unità d’area, sottrazione di aree, rettangolo circoscritto
Punteggi attribuiti su 2170 classi di 20 sezioni:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 6 | 385 (44%) | 267 (30%) | 142 (16%) | 58 (7%) | 24 (3%) | 876 | 0.94 |
| Cat 7 | 267 (37%) | 254 (35%) | 125 (17%) | 51 (7%) | 32 (4%) | 729 | 1.08 |
| Cat 8 | 224 (40%) | 150 (27%) | 85 (15%) | 60 (11%) | 46 (8%) | 565 | 1.21 |
| Totale | 876 (40%) | 671 (31%) | 352 (16%) | 169 (8%) | 102 (5%) | 2170 | 1.06 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
Malgrado la progressione della media dei punteggi da 0,8 a 1,2 dalla categoria 6 alla categoria 8, la risuscita media resta debole. Le osservazioni che seguono sono frutto dell’analisi degli elaborati della Svizzera romanda (146 dei quali: 56 in cat.6, 51 in cat. 7 e 39 in cat 8)
1. Il compito per la risoluzione
Questo compito è lungo e richiede molta precisione. I criteri di attribuzione dei punteggi sono “esigenti” e bisogna dunque relativizzare l’interpretazione delle medie dei punteggi attribuiti. Ci sono molte figure (1 quadrato, 1 rettangolo, da 5 a 6 triangoli differenti a seconda della scomposizione della parte centrale del razzo). Un piccolo errore su una di tali figure implica una penalizzazione di un punto, una spiegazione giudicata non sufficiente implica una penalizzazione di un punto e si può arrivare a soluzioni quasi corrette alle quali vengono attribuiti 2 punti E qui si evidenziano le difficoltà della definizione dei criteri di attribuzione dei punteggi nel caso di un compito complesso.
2. Le procedure
C’è una grande varietà di procedure utilizzate nella determinazione delle aree ed è difficile raggrupparle, visto che possono ancora variare da una figura all’altra. Possiamo comunque identificare qualche grande categoria in generale.
- Alcune spiegazioni parlano di ritaglio e ricomposizione: Si tagliano le forme difficili da calcolare per farne di più facili Bisogna togliere dei pezzi un po’ ovunque per rimetterli da qualche parte per formare un quadrato o un rettangolo. Talvolta le spiegazioni sono accompagnate da uno schema, talvolta c’è solo una somma di misure determinate, talvolta dei colori per precisare la relazione tra una parte della figura e la misura della sua area, …
- Altre spiegazioni non menzionano i ritagli, le ricomposizioni o le compensazioni, ma possiamo o essere pressoché certi che siano state effettuati. In questi elaborati sono menzionate solo le misure di aree parziali vicino alle parti delle figure o segnate con colori con somme per determinare l’area totale.
- Si trovano procedure per “sottrazione” di semi quadrati (triangoli). La figura è inscritta in un quadrato o in un rettangolo da cui si tolgono certe parti. Queste procedure sono efficaci, ma rare (si vedano gli esempi qui di seguito)
Ad esempio: Abbiamo dapprima calcolato l’area del quadrato intorno al fiore. Abbiamo sottratto le parti bianche. 6 × 6 = 36 quadrati 36 – 2 quadrati (4 angoli) = 34 34 – (8 × 2) = 18 quadrati (8 × 2 resto parti bianche)
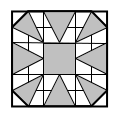
- Conteggio successivo quadrato dopo quadrato
Esempio (Cat 6)
In ciascuna figura gli allievi contano progressivamente i quadrati interi, poi quelli ricomposti. Per il fiore qualche problema di notazione con i numeri 13,5, 14,5, 15, 5 t 16, 5 rettificati tramite l’addizione 16 + 2 = 18, per le foglie le cose vanno meno bene e conducono a 3,95 difficile da interpretare, al posto di 4. Per il razzo i raggruppamenti sono corretti ma è la sistemazione inadeguata del “16” nella parte di destra della base che porta all’errore nel conteggio finale.

- Confronto diretto
I pezzi del fiore sono riportati sul razzo. Questa procedura non porta in generale ad un’area precisa negli elaborati esaminati a causa delle dimensioni di certi triangoli.
L’esempio seguente (Cat 7) dà una buona approssimazione, ma un esame dettagliato mette in evidenza numerose imprecisioni:

- Misure dei lati dei pezzi e calcolo di aree. Questa procedura è favorita dalla dimensione del lato della quadrettatura che, nella maggior parte delle fotocopie date agli allievi è molto vicina a 0,5 cm. È più frequente, sembrerebbe, nelle categorie 7 e 8, piuttosto che nella categoria 6. Gli allievi che gestiscono bene la formula dell’area del triangolo arrivano a risultati approssimati in ragione dei quattro petali degli angoli del fiore che sono dei triangoli in cui nessuno dei lati segue i lati della quadrettatura, o ad altre misure di lati che non sono numeri interi.
3. Gli ostacoli
Si può dire che il conflitto “area/perimetro” sia superato. Fra tutti gli elaborati esaminati solo in due casi sono presi in considerazione i perimetri al posto delle aree.
La determinazione delle aree dei quadrati e dei rettangoli delle figure proposte non presentano pressoché più questo tipo di ostacolo. In quadrati unità si osservano risposte senza notazioni di operazioni (conteggio, evidenziazione...) oppure scritture moltiplicative (2 × 2, 2 × 6, …) In unità usuali (cm2), le scritture delle operazioni sono più frequenti.
La determinazione delle aree dei triangoli isosceli inscritti in un quadrato 2x2 (testa del razzo e quattro petali del fiore) è corretta nella maggior parte degli elaborati.
In unità usuali, la “base” e “l’altezza” sono entrambe di 1 cm e la formula è applicata correttamente. Per i triangoli rettangoli che possono presentarsi nella scomposizione della base del razzo (2 x 3) non si rilevano difficoltà negli elaborati osservati.
Le difficoltà appaiono con i triangoli aventi un angolo ottuso e un lato sulla quadrettatura (foglie del fiore e alettoni del razzo) così come con i triangoli senza lati sulla quadrettatura (petali piccoli).
Per queste figure il metodo per scomposizione e ricomposizione dopo spostamento di pezzi non può che essere approssimativo (salvo per i petali piccoli dove abbiamo trovato una ricomposizione esatta). Gli allievi scompongono i triangoli secondo le linee della quadrettatura e cercano di sistemarli per formare un rettangolo, ma i pezzi di questi puzzle non ne permettono la ricostituzione (e sono troppo piccoli perché ci si renda conto degli errori).
Si tratta di un ostacolo che potrà essere superato solo passando da una procedura “additiva” dove le parti sono ricomposte per giustapposizione a una procedura “sottrattiva” dove la figura è inscritta in un rettangolo le cui parti complementari della figura sono anch’esse triangoli aventi dei lati in comune con quelli dei rettangoli. L'area della figura si calcola per sottrazione dall’area di questi triangoli complementari a quella dell’area del rettangolo. Si passa qui dallo stadio della “manipolazione” a quello di un’operazione mentale sulle misure.
Per esempio nella figura seguente: l’area del triangolo inscritto si calcola per “sottrazione” da quelle dei tre triangoli del rettangolo circoscritto
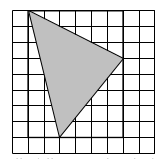
Un altro ostacolo è quello delle approssimazioni nel caso delle misure seguite dal calcolo delle aree: gli allievi non sono coscienti del fatto che i risultati delle loro misure non sono numeri ben determinati bensì degli intervalli. Sulla quadrettatura le misure sono numeri ben determinati, ma sovente sono irrazionali.
Questo problema permette di tornare su alcuni concetti fondamentali necessari alla determinazione delle aree della quadrettatura:
- La distinzione tra le grandezze in gioco: la lunghezza e l’area.
- La necessità di scegliere un’unità “naturale”, il quadretto della quadrettatura e di abbandonare la voglia di misurare le dimensioni delle figure che non permettono di determinare l’area con una precisione sufficiente e che, inoltre, conducono a calcoli fastidiosi e fanno intervenire numeri irrazionali.
- La necessità di ritaglio in figure “elementari” (triangoli, rettangoli, trapezi…) le cui misure dei lati o delle altezze sono determinate in maniera precisa dalla quadrettatura.
- La determinazione delle aree di queste figure elementari a partire dal rettangolo (equivalenza fra rettangolo e parallelogramma, i triangoli o i rombi sono dei semi-parallelogrammi…) per dare un senso alle “formule”. - Le isometrie che intervengono quando si “spostano” parti delle figure per ricomporle in figure con numeri interi di quadretti. Esempio confronto di lunghezze dei lati.
- I confronti di lunghezze di lati e di diagonali che conducono a misure decimali o irrazionali.
- Attività di misurazioni dove venga tenuto conto dei limiti della precisione, poi calcolo di aree con gli estremi inferiori, poi superiori delle “misure” prese, al fine di osservare l’ampiezza degli scarti tra gli estremi delle aree trovate.
- ...
(c) ARMT, 2012-2024