Le tangram du menuisier (I)

Identification

Rallye: 29.II.10 ; catégories: 6, 7 ; domaines: GP, GM
Familles:

• CA - Comparer des aires
• CA/P - Comparer des aires sur un quadrillage
• LA - Utiliser des mesures de longueurs et aires

Envoyer une remarque ou une suggestion

Résumé

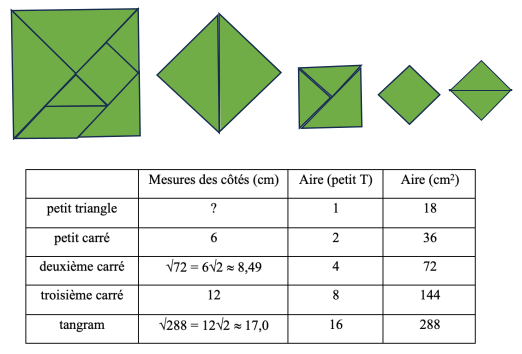
À partir de la photo d’un Tangram et de ses sept pièces, trouver la mesure du côté du Tangram connaissant la mesure du côté de la petite pièce carrée ($6$ cm).

Enoncé

Tâche de résolution et savoirs mobilisés

- Observer la photo et «voir» qu’il s’agit d’un puzzle de 7 pièces: cinq triangles isocèles rectangles (deux grands, un moyen, deux petits) un carré et un parallélogramme, puis analyser les rapports entre les côtés des pièces (côtés égaux de 6 cm, côtés doubles de 12 cm, côtés d'autres mesures) et entre les aires (pièces dont l’aire est le double de celle d’une autre, ...)

- Les savoirs mobilisé sont ceux qui se rapportent aux relations entre les longueurs (figures d'une dimension ou 1D) comme par exemple des côtés égaux, ou entre les aires (figures de deux dimensions ou 2D) comme par exemple l'aire du carré est le double de celle des petits triangle, entre les longueurs et les aires comme par exemple les formules classiques où l'aire (2D) est un produit de deux mesures de longueurs (1D) tout ceci pour chacun des trois types de figures, triangle isocèle rectangle, carré et parallélogramme. Ces savoirs sur chacune des figures doivent ensuite être combinés progressivement avec ceux des figures juxtaposées.

- Un savoir nouveau, particulièrement important dans cette situation est la relation entre le côté (c) et la diagonale d'un carré (d); en termes algébriques: d = c√2. Il se construit en constatant que la diagonale d'un carré est le côté d'un second carré dont l'aire est le double du premier.

Les procédures de résolution sont multiples, en se limitant aux figures d'une dimension (1D):

- par reproduction du dessin en vraie grandeur à partir d’un carré de 6 cm de côté,

- par agrandissement après mesure des dimensions de la figure à la règle garaduée et calcul de "l'échelle" ou "facteur d'agrandissement,

- par l'observation de figures composées ou voisines et des déductions qu'on peut en tirer,

- par mesure. avec la règle graduée, des dimensions non entières comme la diagonale du carré, ou de certains côtés de triangles et du parallélogramme, combinés avec des mesures entières de côtés

En partant de l'espace des longueurs (1D) passer à celui des aires (2D) puis retourner à celui des longueurs, il y a aussi plusieurs procédures :

- calculer l'aire de petit carré de 6 cm de côté : 36 cm$^2$, paver le tangram avec des petits triangles d'aire 18 cm$^2$, pour constater que la partie inférieure droite du tangram a une aire de quatre petits carrés et que l'aire du tangram est celle de 8 carrés ou 288 cm$^2$. et rechercher la mesure du côté du tangram qui est le nombre qui multiplié par lui-même donne $288$, désigné par $\sqrt{288}$ cm, dont une de ses approximations est $\approx 17$ cm ou $\approx 16,97$ cm.

- rechercher la mesure de la diagonale du petit carré, en imaginant un carré d'aire double 72 cm$^2$ (par exemple un carré constitué du triangle moyen et des deux petits juxtaposés) dont le côté est justement la diagonale du petit carré et, comme précédemment, est le nombre qui multiplié par lui-même donne $72$, désigné par $\sqrt{72}$ cm, dont une de ses approximations est $\approx 8,5$ cm. Cette valeur permet de revenir dans l'espace des mesures de longueurs et de calculer la longueur du côté du tangram.

Notions mathématiques

géométrie, tangram, pavage, puzzle, polygone, triangle, carré, diagonale, aire, périmètre, rapport, racine de 2

Résultats

29.II.10

Points attribués, sur 1812 classes de 18 sections:

Selon les critères déterminés lors de l’analyse a priori:

• 4 points: Réponse correcte (la mesure du côté du Tangram est, en cm, $\sqrt{288}$, ou une valeur numérique de 16,9 à 17 cm en cas de détermination par dessin - avec présentation du dessin - ou $\approx 17$ ou $\approx16,97$ ... par la calculatrice ou encore $12\sqrt{2}$ - pour ceux qui auraient retenu la formule $c\sqrt{2}$), avec le détail de toutes les mesures intermédiaires trouvées - d’aires ou de longueurs - et quelques mots pour décrire la démarche comme, par exemple: les petits triangles sont la moitié du petit carré ou le côté du Tangram mesure le double de la diagonale du petit carré interne, avec une justification.
• 3 points: Réponse correcte avec le détail de certaines mesures et description peu claire.
• 2 points: Réponse correcte sans aucune explication ni détails de la procédure
  ou réponse erronée (par exemple avec des erreurs de calcul), avec le détail de certaines mesures intermédiaires et description claire.
• 1 point: Réponse qui se limite à l’aire du Tangram (288 cm$^2$)
  ou mesure proche de 17 (inférieure à 16,8 ou supérieure à 17,1) sans présentation du dessin sur lequel a été prise la mesure
  ou début de recherche cohérent avec quelques mesures ou relations trouvées entre les aires ou les côtés des figures.
• 0 point: Incompréhension du problème.

Procédures, obstacles et erreurs relevés

Les résultats précédents montrent un échec dans près des deux tiers des copies examinées, pour un problème qui peut se résoudre par une simple construction en vraie grandeur.

Lorsque les procédures se déroulent en dans "l'espace à une dimension" sur les segments de droites et périmètres, les erreurs sont dues aux imprécisions des mesures prises à la règle graduée ou à la construction en vraie grandeur. Elles sont multiples et décrites dans plusieurs articles rédigés à la suite d'analyses a posteriori des copies des élèves. (Voir Bibliographie)

Lorsque les élèves passent par "l'espace à deux dimension" et travaillant sur les aires d'une ou de certaines pièces, on relève des difficultés à réaliser un pavage du tangram par 16 petits triangles ou par 8 carrés. Lorsque l'aire du tangram est trouvée (288) il y a encore de nombreuses difficultés à se rendre compte que cette mesure d'aire est le produit de deux mesures à une dimension: le côté par lui-même (mesure qui pourrait s'approcher par essais successifs ou par l'extraction de la racine carrée.)

Un obstacle essentiel, pour l'un ou l'autre type de procédure, et l'impossibilité d'écrire la mesure cherchée sous forme décimale finie ou de se rendre compte qu'on aborde de nouveaux nombres. Les réponses du genre le côté mesure 16,9705627485 cm sont fréquentes et témoignent d'une méconnaissance totale des estimations ou de la réalité d'une construction de l'objet "tangram".

Exploitations didactiques

Cette activité présente les mêmes possibilités d'exploitations didactiques que Le tangram du menuisier (II) (29.II.17);

Le tangram est un objet d'une grande richesse didactique qui permet de couvrir une grande partie du programme de géométrie plane de la scolarité obligatoire : les concepts d'aire (2D) et de longueur (1D); les rapports entre les mesures correspondantes de ces grandeurs; l'étude de polygones élémentaires ; les isométries (translations, rotations et symétries axiales), les similitudes et leurs rapports, les nombres rationnels et irrationnels, les approximations, les premières expressions littérales lorsqu'on passe au cas général du côté u de la seconde version ; ...

De quoi donner du sens aux activités géométriques, des premières années de l'école primaire à la fin du secondaire inférieur.

Pour aller plus loin

Exemples d'activités en vue d'un parcours didactique avec la classe

À expérimenter en classe, selon des modalités déterminées par l'enseignant; avec envoi de description et commentaires pour rendre compte de l'opportunité de l'activité pour la construction des savoirs (notés en italique).

a) Faire dessiner le tangram de la figure de l'énoncé (côté du carré de 6 cm) sur papier quadrillé 5 x 5 mm.

Apprendre à utiliser la trame du quadrillage pour une construction précise, avec rotation de la figure de l'énoncé de 45 degrés pour que les côtés du carré correspondent aux droites du quadrillage. Constater qu'il y a plusieurs côtés de pièces alignés, ce qui évite de tracer tous les segments de droite. Reconnaître des droites et côtés parallèles et perpendiculaires.

b) Demander de trouver tous les carrés et les triangles de dimensions différentes, que l'on peut composer avec une ou plusieurs pièces du tangram, et de les dessiner.

Observer et reconnaître des polygones élémentaires.

c) Dresser la liste des figures possibles et différentes formées de deux des sept pièces du tangram juxtaposées par un côté entier commun.

Reconnaître les côtés de même longueur pour établir un inventaire organisé et complet, par déduction logique.

d) Etablir un tableau (6 x 6) des cinq pièces différentes et du tangram entier qui donne l'aire de chacune des 6 figures en fonction de chacune des autres prise comme unité.

Par exemple Les quatre carrés

Décomposition de polygones en différentes unités d'aire. Expression des rapports et de leurs inverses par des nombres rationnels, fractions, approximations décimales.

e) Trouver toutes les longueurs différentes des côtés des pièces et du tangram entier, les classer par ordre de grandeur et les exprimer en cm (puis en unité u pour la seconde version). En particulier donner l'écriture exacte des longueurs qui ne sont pas des nombres rationnels et le rapport entre la longueur d'un côté de carré et celle de sa diagonale.

Approche de l'écriture d'une longueur irrationnelle à l'aide du signe √ ; (l'écriture √2 peut être remplacée par une de ses approximations : 1,4 ou 1,5 pour les jeunes élèves.

f) Classer les 5 pièces différentes du tangram dans l'ordre de grandeur de leur périmètre.

Addition de mesures de longueurs rationnelles et irrationnelles qui demande des approximations.

g) Trouver les polygones convexes que l'on peut composeravec les 7 pièces du tangram.

Il y en a 13, de même aire mais de périmètres différents. Leur recherche est une activité intense de mise en oeuvre des relations entre unités de longueurs permettant de mieux maîtriser les rapports entre un nombre et sa racine carrée.

Autres problèmes de la BPrmt :

- Partage d'un carré (20.I.19);

- Le partage du rectangle (30.I.18);

- Une mosaïque du Maroc (27.II.18);

- Les sept polygones (29.I.18);

Bibliographie

Gruppo geometria per i grandi : Paola Bajorko, Brunella Brogi, Fabio Brunelli, Federica Curreli, Speranza Dettori, Florence Falguères, Lucia Grugnetti, François Jaquet, Elisabetta Mari, Elsa Renna, Patrizia Sabatini, M. Agostina Satta, Cinzia Utzeri, Vincenza Vannucci. Da sette poligoni a ... sette poligoni / De sept polygones à … sept polygones IN Gazette de Transalpie no 12, pp. 41-83. (Analisi a posteriori del problema “I sette poligoni” e delle due versioni del problema “Il Tangram del falegname” / Analyse a posteriori du problème « Les sept polygones » et de deux versions du problème « Le Tangram du menuisier »)

Jaquet. F. Les apports du RMT. 2024. IN Gazette de Transalpie no 15, pp. 29-56