
Banca di problemi del RMT
gp179-it
 |
Banca di problemi del RMTgp179-it |
|
Envoyer une remarque ou une suggestion
Determinare il numero dei punti nascosti da un foglio bianco, sovrapposto ad un rettangolo che contiene due reti punteggiate
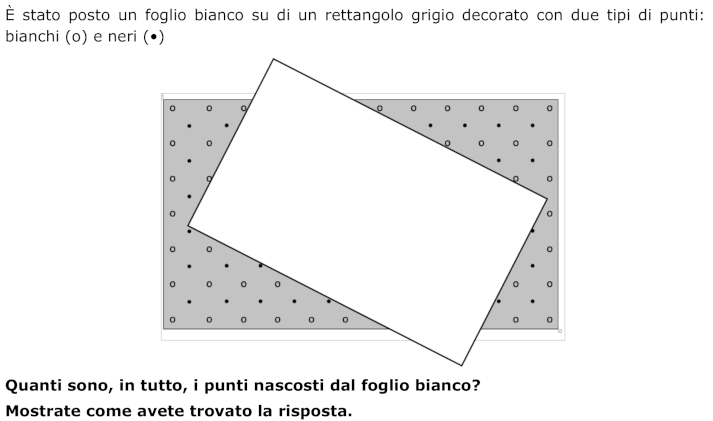
Riconoscere le due reti di punti sfalsate e gli allineamenti dei loro punti.
Le conoscenze in gioco sono il conteggio uno a uno dei punti di ciascuna griglia nelle due direzioni e, per le altre procedure, l’addizione ripetuta o la moltiplicazione.
- Una procedura consiste nel completare le due reti di punti del rettangolo grigio, disegnandole sul foglio bianco (il che esige, per essere efficace, molta precisione e un disegno con l’aiuto di un righello per gli allineamenti).
- Per evitare il disegno ci sono altre procedure che ricorrono alle regolarità delle reti di punti e alle enumerazioni per righe e per colonne per determinare il numero totale dei punti del foglio e trovare il numero di punti nascosti per sottrazione dei punti visibili.
- Ci sono 84 punti bianchi (7 × 12) 66 neri (6 × 11); 150 in totale. I punti visibili sono 61 (38 + 23). Ci sono dunque 89 punti nascosti (150 – 61).
conteggio, linea, allineamento, griglia, moltiplicazione, sottrazione
Punteggi attribuiti, su 929 classi di 6 sezioni:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 4 | 89 (16%) | 269 (49%) | 65 (12%) | 53 (10%) | 78 (14%) | 554 | 1.57 |
| Cat 5 | 69 (13%) | 208 (39%) | 71 (13%) | 79 (15%) | 111 (21%) | 538 | 1.92 |
| Totale | 158 (14%) | 477 (44%) | 136 (12%) | 132 (12%) | 189 (17%) | 1092 | 1.74 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
Gli elaborati osservati (circa 200 della sezione SI) rivelano solo le due procedure menzionate nel compito di risoluzione: da un lato il disegno dei punti nascosti e/o il loro conteggio riga per riga, dall'altro il calcolo del numero totale di punti sul foglio grigio mediante moltiplicazione e addizione seguite da sottrazione del numero di punti visibili.
Nonostante la semplicità della scelta delle procedure, sono gli errori a rivelare gli ostacoli incontrati perché solo il 20% delle copie dà la risposta esatta “89 punti nascosti” e circa il 15% dà risposte con 87, 88, 90 o 91 punti nascosti.
Le procedure mediante il disegno dei punti nascosti (che compaiono in circa la metà degli elaborati esaminati rivelano un ostacolo sottovalutato durante l'analisi a priori del problema e anche nella sua prima versione quasi 30 anni fa [[ pb:gp19-fr|La macchia (03 .II.06, cat 3, 4, 5)]]: il concetto di rete di punti "a griglia" è lungi dall'essere costruito nelle categorie 4 e 5. Quelli che hanno concepito il problema non immaginavano la portata del lavoro di costruzione di questa rete che è una delle conoscenze in gioco. Alcune copie testimoniano una percezione delle due reti bianca e nera e dei loro allineamenti orizzontali e verticali. (esempi 1 e 2).
Quindi, senza una chiara percezione delle linee, il conteggio diventa casuale. (Esempi 3 e 4)
Esistono ancora procedure di calcolo sugli allineamenti verticali o orizzontali, siano essi disegnati o meno. (esempio 5)
In tutti gli elaborati si nota l'importanza che alcuni allievi attribuiscono alle distanze tra i punti (esempio 6) o al loro allineamento su rette o entrambi contemporaneamente. Lo strumento “righello” ha infatti due funzioni: dal lato graduato, per effettuare misurazioni di lunghezza, e dal lato non graduato per modellare la linea. Gli allievi che tengono conto solo di una delle due direzioni e riportano le lunghezze non si rendono conto che l'altra dimensione dà l'allineamento.
Tutte queste osservazioni permettono di affermare che la nozione di “allineamento” o, più in generale di “linea dritta” come supporto all'allineamento non è “innata” ma è “da costruire” per molte allievi du categorie 4 e anche 5, meno frequentemente.
Le procedure di calcolo (moltiplicazioni e sottrazioni di punti visibili) sono meno numerose, ma più efficaci. Gli errori sono nel conteggio dei punti visibili (60 o 62 invece di 61), nel conteggio delle colonne (11 invece di 12 per i punti bianchi e 10 invece di 11 per i punti neri).

L'osservazione degli elaborati rivela una progressione nella costruzione del concetto di “rete di punti” (i bianchi e i neri) del rettangolo grigio della figura riportata nella formulazione del problema. Queste due reti sono i vertici delle griglie. Da un punto di vista didattico, queste conoscenze sembrano a prima vista “elementari”, “ovvie”, “naturali” o così comuni da non essere considerate “necessarie” nell'ambito di un programma scolastico. “Non perderemo tempo guardando la carta millimetrata che gli studenti usano ogni giorno! »
Il problema Punti nascosti richiede un lavoro di costruzione che va oltre le osservazioni o le percezioni visive che emergeranno durante la fase di dibattito tra gruppi di allivi o di istituzionalizzazione da parte dell'insegnante. È assolutamente necessario che ogni allievo disegni le due reti stendendole sul foglio bianco della figura: deve disegnare con precisione le linee parallele, capendo che sono determinate dai punti della parte visibile del rettangolo grigio, deve capire che le distanze tra due punti vicini della stessa linea sono uguali, che le due direzioni delle linee sono perpendicolari. Poi deve essere in grado di verificare che ci sono effettivamente 89 punti nascosti (e non 88 o 90) e che esiste un modo per calcolare i punti totali mediante moltiplicazione e addizione (7 × 12) + (6 × 11) = 150 e che esiste una relazione tra questo numero (150), il numero di punti visibili (61) e il numero di punti nascosti.
Questo disegno preciso è essenziale per la costruzione di questa conoscenza della rete di punti ai vertici di una griglia che utilizza i concetti di retta, parallela, perpendicolare, distanza costante e percezione visiva.
Una proposta di attività, per rompere le abitudini con la rete di punti rettangolari, orizzontalità e verticalità; comprendere che è necessario scegliere un punto di partenza, tracciare una prima retta passante per questo punto e tracciare le altre a distanza costante (misurazione con righello graduato o, meglio, mediante trasferimento con compasso); tracciare una seconda retta passante per il punto prescelto, perpendicolare alla prima, sempre con punti equidistanti; poi disegna paralleli e perpendicolari....
Riproducete su un foglio di carta bianco la seguente figura:
