ARMT

Banca di problemi del RMT

gp182-it

 centre

Cibo per tutti!

Identificazione

Rally: 31.F.03 ; categorie: 3, 4, 5 ; ambito: GP
Famiglie:

Envoyer une remarque ou une suggestion

Sunto

Elencare tutti i diversi percorsi che partono da un punto e tornano al punto di partenza, collegando i cinque nodi di una rete senza passare due volte per lo stesso.

Enunciato

Compito per la risoluzione e saperi mobilizzati

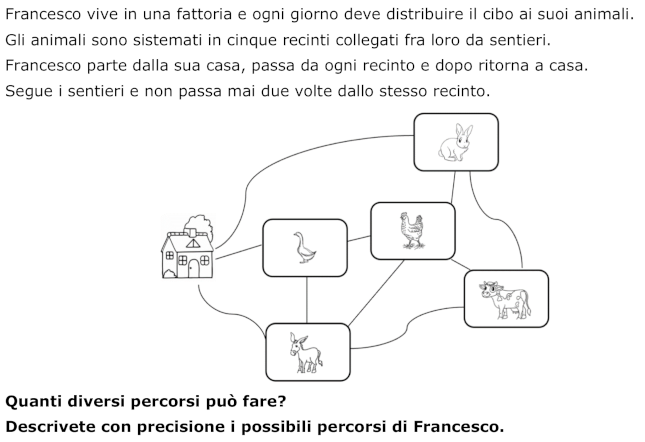
- Rendersi conto che Francesco deve passare da ogni recinto una sola volta, percorrendo i sentieri e partendo dalla casa per ritornarvi alla fine del percorso.

- Trovare un modo per elencare tutte le soluzioni: disegni, elenchi, abbreviazioni, …

- Procedere per tentativi più o meno organizzati.

- Posto O=oca, G=gallina, A=asino, C=coniglio, M=mucca, trovare le 10 soluzioni, perché ognuno dei 5 percorsi può essere seguito in un verso o nell'altro: 

  OGAMC, OGCMA, OAGMC, OAMGC, AOGMC, AMCGO, CMAGO, CMGAO, CGMAO, CMGOA.

Nozioni matematiche

percorso, calcolo combinatorio, rete, enumerazione

Risultati

31.F.03

Points attribués sur la base de copies de ... classes de 18 sections:

Categoria01234Nb.classiMedia
Cat 321 (35%)17 (28%)13 (22%)6 (10%)3 (5%)601.22
Cat 415 (22%)18 (26%)19 (28%)8 (12%)8 (12%)681.65
Cat 55 (8%)18 (30%)19 (32%)7 (12%)11 (18%)602.02
Totale41 (22%)53 (28%)51 (27%)21 (11%)22 (12%)1881.63
Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema.

Secondo i criteri dell’analisi a priori :

  • 4 punti: I 10 percorsi descritti o disegnati in modo chiaro senza errori né doppioni
  • 3 punti: I 10 percorsi descritti o disegnati in modo chiaro con al massimo due errori o doppioni
    oppure 8 o 9 percorsi descritti o disegnati in modo chiaro senza errori né doppioni.
  • 2 punti: Risposta «10 percorsi» senza alcuna descrizione
    oppure 8 o 9 percorsi descritti o disegnati in modo chiaro che includono al massimo due errori o doppioni
    oppure 6 o 7 percorsi descritti o disegnati in modo chiaro senza errori né doppioni
  • 1 punto: 6 o 7 percorsi descritti o disegnati in modo chiaro che includono al massimo due errori o doppioni
    oppure 4 o 5 percorsi descritti o disegnati in modo chiaro senza errori né doppioni
  • 0 punto: Meno di 4 percorsi
    oppure incomprensione del problema

Procedure, ostacoli ed errori rilevati

Delle venti elaborati esaminati non sono state notate strategie caratteristiche. Sembra che i percorsi si trovino senza un'organizzazione sistematica.

Questo inventario dei sentieri risulta difficile nella categoria 3.