Partage d’un carré (bis)

Identification

Rallye: 31.II.16 ; catégories: 8, 9, 10 ; domaine: GP
Familles:

• RD - Rechercher ou utiliser des dimensions
• RD/AP - Déterminer des aires et/ou périmètres

Envoyer une remarque ou une suggestion

Résumé

Calculer l’aire d’un carré dans lequel deux segments issus d’un point d’un côté aux deux sommets opposés du carré mesurent chacun 10 cm.

Enoncé

Tâche de résolution et savoirs mobilisés

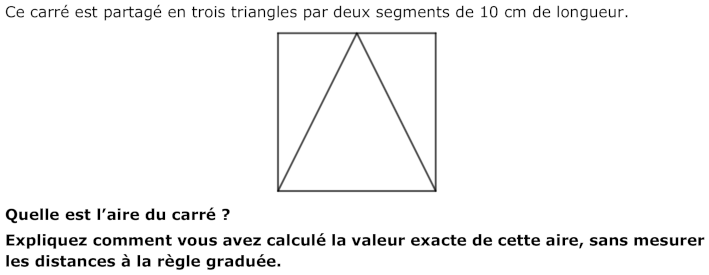
- Observer la figure et constater que le grand triangle est isocèle, que les deux petits triangles sont égaux, rectangles et dont le petit côté est la moitié du grand côté de l’angle droit (ou des demi-rectangles de 5 × 10)

- Établir alors la relation de Pythagore dans l’un des deux triangles rectangles, par exemple en désignant par c la mesure du petit côté de l’angle droit, le grand côté mesure 2c et la relation c$^2$ + (2c)$^2$ = 100 devient 5c$^2$ = 100 puis c$^2$ = 20 et l’aire du carré 4 c$^2$ = 80.

Les savoirs mobilisés sont la relation de Pythagore, l'élévation au carré et l'extraction de la racine carrée et, le plus important, la conscience que la racine carrés d'un nombre est différente de toutes ses approximations décimales. C'est-à-dire que si l'on élève au carré une approximation de la racine carrée d'un nombre, on n'obtiendra pas ce nombre.

Notions mathématiques

géométrie, carré, aire, triangle isocèle, triangle rectangle, Pythagore, équation

Résultats

31.II.16

Résultats sur 1186 classes de 20 sections:

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Réponse correcte « l’aire du carré est 80 cm$^2$ » avec description détaillée des calculs (reconnaissance des rectangles 1 × 2 et application de Pythagore)
• 3 points: Réponse correcte mais avec explications peu claires
  ou réponse approximative (par exemple 79,92 cm$^2$) due à l’usage d’écritures décimales de √20 ou d’autres nombres irrationnels, avec explications claires
• 2 points: Réponse correcte sans explications
  ou reconnaissance du rapport 1/2 mais erreur dans la pose de l’équation avec réponse cohérente
• 1 point: Début de raisonnement cohérent (perception du rapport 1/2 entre les dimensions des côtés des triangles rectangles)
  ou réponse obtenue par mesure sur un dessin du carré
• 0 point: Incompréhension du problème

Procédures, obstacles et erreurs relevés

Ce problème est une variante de Partage d'un carré (20.I.19) ou le carré de base est réparti en quatre triangles par trois segments de 10 cm alors que, dans cete deuxième version, la répartition se fait selon deux segments de 10 cm, en trois triangles.

Les résultats pour les catégories 9 et 10 sont légèrement meilleurs mais avec encore un pourcentage d'échecs important.

Une analyse a posteriori des 59 copies classes de catégorie 8 de la section SR (avec sélection scolaire dès les catégories 6 ou 7, ce qui entraîne une moyenne des points attribués de 1,5 supérieure à 0,8 pour l'ensemble des classes participantes) permet de distinguer :

- 14 copies avec une réponse "80 cm$^2$" obtenue par la résolution décrite dans la rubrique "Tâche de résolution et savoirs mobilisés"

Dans deux cas, cependant, une approximation intermédiaire est donnée après l'extraction de la racine carrée du côté x = √20 $\approx 4,47$ mais on ne peut pas savoir si la réponse 80 a été trouvée en calculant le carré de l'approximation 8,94 et en l'arrondissant à 80 ou si les élèves ont effectué l'opération (2√20)$^2$ = 4 x 20 = 80 (Voir figure 1)

- 6 copies avec une réponse proche de "80 cm$^2$" obtenue après avoir calculé correctement la racine carrée de 80 ou de 20 et poursuivi les opérations (Voir figure 2) ) ou avec des approximations "excessives" comme 8,94428 pour le côté du carré, obtenu par extraction de √80 à la calculatrice et 80,00014472 après élévation au carré.

- 8 copies avec une réponse proche de 67 cm$^2$". Soit il s'agit d'une erreur dans l'équation x$^2$ + x$^2$/2 = 100 où (x/2)$^2$ n'est pas x$^2$/4. Soit l'aire d'un des triangles rectangle est considéré comme le tiers de 100.

- 7 copies avec réponse 100 ou 200 cm$^2$. (C'est très facile à calculer, si l'on considère que le grand triangle est équilatéral)

- 3 copies avec réponse 75 cm$^2$, en pensant que le petit côté des deux triangles rectangles mesure 5 cm, la moitié de 10.

- 5 copies avec réponse 50 cm$^2$, après décomposition du carré en deux rectangles isométriques dont les deux diagonales mesurent 10 cm, puis application de la relation de Pythagore dans le triangle de côtés 5; 5; et c (côté du carré) non rectangle, pour trouver que c = √50.

- Les 16 autres copies illustrent la richesse d'imagination de stratégies erronées par ces groupes d'élèves: recours à la trigonométrie, applications fantaisistes de la relation de Pythagore, triplet pythagoricien (6; 8; 10), ...

Exploitations didactiques

L'observation des erreurs montre les pistes d'exploitation de l'activité, comme "remédiations"

- travail sur les approximations

- prise de conscience de la relation entre un nombre et sa racine carrée qui ne peut pas s'afficher entièrement sur l'écran de la calculatrice et, par conséquent doit s'écrire avec le symbole √.

- conditions d'application de la relation de Pythagore (valide seulemet pour les triangles rectangles

- élévation au carré de fractions (le numérateur comme le dénominateur)

- ...

mais aussi comme mise en oeuvre des savoirs "revisités" dans d'autres situations:

- Partage d'un carré (20.I.19);

- Le tanrgam du menuisier (II) (29.II.17);

- Le partage du rectangle (30.I.18);

- Une mosaïque du Maroc (27.II.18);

- Les sept polygones (29.I.18);