Suddivisione di un quadrato

Identificazione

Rally: 31.II.16 ; categorie: 8, 9, 10 ; ambito: GP
Famiglie:

• RD - Ricercare o utilizzare dimensioni
• RD/AP - Determinare aree e/o perimetri

Envoyer une remarque ou une suggestion

Sunto

Calcolare l’area di un triangolo rettangolo la cui ipotenusa misura 10 cm e il cateto minore misura la metà del cateto maggiore.

Enunciato

Compito per la risoluzione e saperi mobilizzati

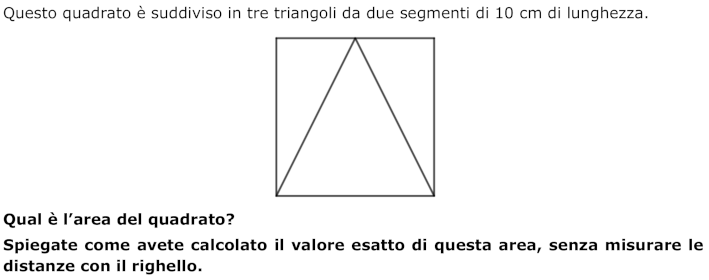
- Osservare la figura e constatare che il triangolo centrale è isoscele, che i due triangoli laterali sono uguali, rettangoli e con il cateto minore che è la metà del cateto maggiore (o dei semirettangoli 5 × 10, le cui dimensioni stanno nel rapporto 1: 2).

- Stabilire allora la relazione di Pitagora per uno dei due triangoli rettangoli, per esempio, chiamando c la misura del cateto minore, il cateto maggiore misurerà 2c e la relazione è c$^2$ + (2c)$^2$ = 100 che diventa 5c$^2$ = 100 poi c$^2$ = 20 e l’area del quadrato 4c$^2$ = 80.

I saperi mobilitati sono la relazione pitagorica, l'elevazione al quadrato e l'estrazione della radice quadrata e, soprattutto, la consapevolezza che la radice quadrata di un numero è diversa da tutte le sue approssimazioni decimali. Cioè, se eleviamo al quadrato un'approssimazione della radice quadrata di un numero, non otterremo quel numero.

Nozioni matematiche

geometria, quadrato, area, triangolo isoscele, triangolo rettangolo, Pitagora, equazione

Risultati

31.II.16

Punteggi attribuiti su 1186 classi di 20 sezioni:

Secondo i criteri dell’analisi a priori :

• 4 points: Risposta corretta “l’area del quadrato è 80 cm2” con descrizione dettagliata dei calcoli (riconoscimento dei rettangoli 1 × 2 e applicazione del teorema di Pitagora)
• 3 points: Risposta corretta ma con spiegazioni poco chiare
  oppure risposta approssimativa (per esempio 79,92 cm2) dovuta all’uso della scrittura decimale di √20 o di altri numeri irrazionali, con spiegazioni chiare
• 2 points: Risposta corretta senza spiegazioni
  oppure riconoscimento del rapporto 1/ 2 con errori nell’impostazione dell’equazione, con risposta coerente
• 1 point: Inizio di ragionamento corretto (percezione del rapporto 1/ 2 tra i cateti dei triangoli rettangoli)
  oppure risposta ottenuta con le misure prese dal disegno del quadrato
• 0 point: Incompréhension du problèmeRE

Procedure, ostacoli ed errori rilevati

I risultati per le categorie 9 e 10 sono leggermente migliori ma con ancora una percentuale significativa di fallimenti.=

Questo problema è una variante di Divisione di un quadratole (20.I.19) dove il quadrato di è diviso in quattro triangoli da tre segmenti di 10 cm mentre, in questa seconda versione, la divisione è fatta secondo due segmenti di 10 cm, in tre triangoli.

I risultati per le categorie 9 e 10 sono leggermente migliori ma con ancora una percentuale significativa di fallimenti.

L'analisi a posteriori delle 59 copie delle classi di categoria 8 della sezione SR (selezionate dalle categorie 6 o 7, determina una media di punteggi attribuiti di 1,5, maggiore di 0,8 per tutte le classi partecipanti) consente di distinguere:

- 14 elaborati con una risposta "80 cm$^2$" obtenuta dalla risoluzione descritta nella rubrica "Compito di risoluzione e saperi mobilitati"

In due casi però si dà un'approssimazione intermedia dopo aver estratto la radice quadrata del lato x = √20 $\approx 4,47$ ma non si sa se la risposta 80 è stata trovata calcolando il quadrato dell'approssimazione 8,94 e arrotondandolo a 80 o se gli allievi hanno eseguito l'operazione (2√20)$^2$ = 4 x 20 = 80 (Vedi figura 1)

- 6 elaborati con risposta prossima a "80 cm$^2$" ottenuta dopo aver calcolato correttamente la radice quadrata di 80 o di 20 e proseguendo le operazioni (Vedi figura 2)) o con approssimazioni "eccessive" come 8.94428 per il lato del quadrato , ottenuto estraendo √80 con la calcolatrice e 80.00014472 dopo averla elevato al quadrato.

- 8 elaborati con una risposta prossima a 67 cm$^2$". Sia si tratta di un errore nell'equazione x$^2$ + x$^2$/2 = 100 dove (x/2)$^2$ non è x$^2$/4. Sia l'area di uno dei triangoli rettangoli è un terzo di 100.

- 7 elaborati con una risposta 100 ou 200 cm$^2$. (Questo è molto facile da calcolare, considerando che il triangolo grande è equilatero).

- 3 elaborati con una risposta 75 cm$^2$, pensando che il lato corto dei due triangoli rettangoli misura 5 cm, la metà di 10.

- 5 elaborati con una risposta 50 cm$^2$, dopo scomposizione del quadrato in due rettangoli isometrici le cui due diagonali misurano 10 cm, quindi applicazione della relazione pitagorica al triangolo di lato 5; 5; e c (lato del quadrato) non rettangolo, per trovare che c = √50.

- Le altri 16 elaborati illustrano la ricchezza di immaginazione delle strategie errate di questi gruppi di allievi: uso della trigonometria, applicazioni fantasiose della relazione pitagorica, tripletta pitagorica (6; 8; 10), ...

Indicazioni didattiche

L’osservazione degli errori mostra strade per sfruttare l’attività, come la “rimediazione”

- lavorare sulle approssimazioni

- consapevolezza del rapporto tra un numero e la sua radice quadrata che non può essere visualizzata completamente sullo schermo della calcolatrice e, pertanto, deve essere scritta con il simbolo √.

- condizioni di applicazione della relazione pitagorica (valida solo per i triangoli rettangoli

- elevazione al quadrato di frazioni (sia al numeratore che al denominatore)

- ...

ma anche come implementazione di conoscenze “rivisitate” in altre situazioni:

- Divisione di un quadrati (20.I.19);

- Il tanrgam del falegname (II) (29.II.17);

- Suddivisione di un quadrato (30.I.18);

- Un mosaico del Marocco (27.II.18);

- I stte poligoni (29.I.18);