La fourmi s'est perdue

Identification

Rallye: 30.II.19 ; catégories: 9, 10 ; domaine: GP
Familles:

• RD - Rechercher ou utiliser des dimensions
• RD/CER - Traiter des grandeurs liées au cercle
• SF - Etudier des suites de figures

Envoyer une remarque ou une suggestion

Résumé

Complétez le dessin d'un chemin en zigzag convergent en un point et calculez sa longueur, à partir des deux premiers segments (125 et 100)

Enoncé

Tâche de résolution et savoirs mobilisés

Analyse de la tâche a priori

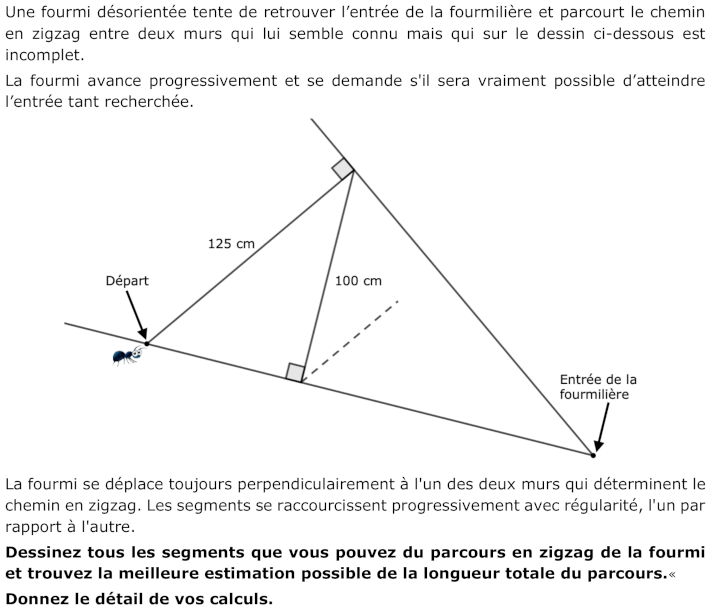
- L'appropriation du problème demande est d'essayer de percevoir le chemin de la fourmi. En ce qui concerne le chemin, comprendre comment il se construit en analysant la figure présentée et en s'appuyant sur les indications de l'énoncé (segments de plus en plus courts) et les indications contenues dans la question : dessinez tous les segments que vous pouvez).

- Une fois que les segments suivants sont reconnus perpendiculaires à l'un ou l’autre des deux murs, les dessiner ... et, à un certain point se demander comment continuer, étant donné que les segments seront toujours plus courts et progressivement "impossibles" à tracer. Avec un dessin sur papier quadrillé à partir du segment initial qui peut être redimensionné à 12,5 cm (25 cases), il est possible de dessiner nettement jusqu'au 15ème segment.

- Comprendre donc que le chemin continue et ne permet pas d'atteindre le petit trou de la fourmilière avec un nombre fini de segments, compte tenu également du "doute" de la petite fourmi de pouvoir atteindre « l’entrée tant recherchée »

En ce qui concerne la recherche de la longueur du parcours, les démarches sont variées et vont des plus accessibles à des démarches plus élaborées pouvant être construites dans une activité de classe ultérieure.

- La démarche la plus accessible consiste à comprendre que le rapport entre les longueurs de deux segments consécutifs du chemin est constant (par exemple en observant que les triangles rectangles qui se forment sont semblables entre eux, ou comprendre comment passer de 125 à 100 et trouver le rapport 4/5) et calculer progressivement les longueurs des différents segments en tenant compte que chaque longueur s'obtient en multipliant la précédente par le rapport constant 4/5 soit par 0,8, donc après 125 et 100 on obtient : 80 ; 64 ; 51,2 ; 40,96 ; 32,768 ; 26,214 ; 20,972, 16,777; 13,422 ; 10,737 ; 8,590 ; 6,872 ; 5 498… (en cm).

Comprendre donc que la procédure d'addition peut continuer indéfiniment mais que les termes de l’addition deviennent de plus en plus petits et donc que la somme croît de moins en moins. Décider ensuite où s’arrêter en tenant compte de la taille de la fourmi ou du dessin. Par exemple, si l'on s'arrête au 15ème terme (qui, avec le dessin, correspond au segment qu'on peut encore tracer clairement) on obtient environ 603 (en cm) Cette procédure permet de trouver "uniquement" une approximation de la longueur du chemin. Par exemple, en ajoutant les valeurs précédentes on trouve 603,009.

- Une procédure avec les mesures des segments sur un dessin est également possible, à condition que ce dessin soit précis et à l'échelle. Le premier triangle rectangle aura des côtés, par exemple, exprimés en mm, de longueurs respectives 125, 100 et 75 (avec le théorème de Pythagore). Dans ce cas, en lisant les mesures approchées au mm, on arrive à environ 610 mm avec 16 à 17 segments.

Ou, avec des connaissances relatives à la somme d'une progression géométrique, éventuellement acquises au niveau de la catégorie 10, en ayant recours au rapport entre les longueurs des segments, considérer la somme de la progression, en tenant compte « intuitivement » que les termes tendent vers 0

S = 125 + 125(4/5) + 125 (4/5)$^2$ +…

Puis en multipliant les deux côtés par 4/5 : (4/5)S = 125(4/5) + 125 (4/5)$^2$ +… et en écrivant la différence entre les deux relations on obtient : S - (4/5)S = 125 et enfin S = 625.

Ou, compte tenu de la configuration géométrique de la ligne brisée, avec les deux séquences de segments parallèles entre elles :

Envisager la proportionnalité entre la longueur de la suite S et la longueur du premier segment et la longueur de la suite moins le premier segment et le deuxième segment : S/125 = (S-125)/100, ce qui conduit à S = 625 (en mm) (procédure qui pourrait être considérée comme une généralisation de la similitude).

En vue d'une éventuelle activité en classe après l’épreuve, il pourrait être intéressant de "construire" les deuxième et troisième procédures avec les élèves pour observer également que, dans ces deux cas, on obtient la longueur effective de la ligne brisée, alors qu’avec le premier on s’en rapproche de plus en plus, mais le processus "ne s'arrête pas" !

Notions mathématiques

progression géométrique, similitude, rapport, raison, limite, approximations, idée d’infini, convergence d’une série, Thales

Résultats

30.I.19

sur 363 classes de 10 sections

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Réponses correctes, (dessin tenant compte de la perpendicularité requise et faisant allusion à "l'impossibilité de le terminer" comme le suggèrent l'énoncé et la question ; avec un chemin qui atteint au moins le 14e ou le 15e segment et une longueur approximative supérieure à 600 cm, mais inférieure à 625 cm) avec les détails des calculs à la fois avec l'identification du rapport et avec les mesures avec un dessin à l'échelle
• 3 points: Réponses correctes, avec le détail des calculs incomplet
  ou dessin correct jusqu'au 12e ou 13e segments au moins et longueur de la ligne brisée légèrement inférieure à 600 cm (entre 580 et 600 cm) avec calculs détaillés
• 2 points: Réponses correctes, sans le détail des calculs
  ou dessin correct jusqu'au 10e ou 11e segments au moins et longueur comme la somme des longueurs des segments trouvés avec une erreur de calcul ou de mesure pouvant être déduite du détail présenté
  ou dessin corrigé jusqu'au 12e ou 13e segments avec un calcul ou des mesures cohérentes
• 1 point: Début de raisonnement correct (dessin avec au moins six segments ou calcul des longueurs mais la somme n'est pas calculée, ...)
  ou identification de la longueur du troisième segment avec un rapport correct
  ou réponse du genre : puisqu’il y a une infinité de termes, la longueur est infinie, avec au moins un début de dessin correct
• 0 point: Incompréhension du problème

Pour aller plus loin

Grugnetti L., Rizza A. con il contributo di Federica Curreli e Cinzia Utzeri. (2024). PROBLEMA “A ZIG ZAG”/PROBLÈME « Á ZIG ZAG » In Gazette de Transalpie / Gazzetta del Translpino 14 pp 47-60