La formica si è persa

Identificazione

Rally: 30.II.19 ; categorie: 9, 10 ; ambito: GP
Famiglie:

• RD - Ricercare o utilizzare dimensioni
• RD/CER - Gestire grandezze della circonferenza
• SF - Studiare successioni di figure

Envoyer une remarque ou une suggestion

Sunto

Completare il disegno di un percorso a zig zag convergente in un punto e calcolarne la lunghezza, sia tramite il rapporto tra le misure di due segmenti successivi a partire dai primi due (125 e 100) (progressione geometrica), sia con disegno e misure.

Enunciato

Compito per la risoluzione e saperi mobilizzati

Analisi del compito a priori

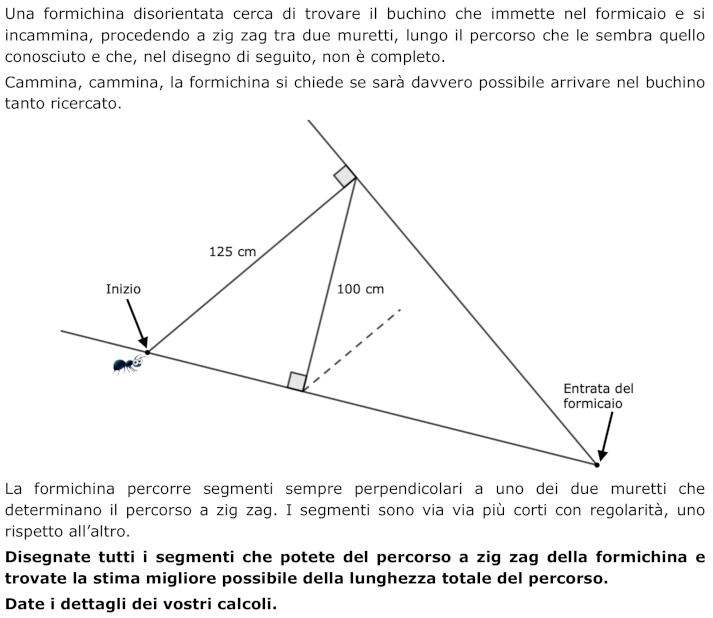
- L’appropriazione del problema richiede che si cerchi di capire come sia fatto il percorso della formichina.

- Per quel che riguarda il percorso, capire come sia costruito mediante l’analisi del disegno presentato e con il supporto delle indicazioni dell’enunciato (segmenti via via più corti con regolarità) e indicazioni contenute nella consegna: disegnate tutti i segmenti che potete).

- Una volta capito che i segmenti successivi sono perpendicolari a una delle due bordure, disegnarli e ... a un certo punto chiedersi come si possa proseguire, visto che i segmenti saranno sempre più corti e via via “impossibili” da tracciare. Con un disegno su carta a quadretti a partire dal segmento iniziale che in scala può essere di 12,5 cm-(25 quadretti) si riesce a disegnare in modo chiaro fino al 15º segmento.

- Capire quindi che il percorso prosegue e non permette di raggiugere con un numero finito di segmenti il buchino del formicaio, anche tenuto conto del “dubbio” della formichina di poter raggiungere il “buchino ricercato”.

Per quel che riguarda la ricerca della lunghezza del percorso, le procedure sono svariate e vanno dalla più abbordabile agli allievi a procedure più elaborate che potranno essere costruite in una successiva attività in classe.

- La démarche la plus accessible consiste à comprendre que le rapport entre les longueurs de deux segments consécutifs du chemin est constant (par exemple en observant que les triangles rectangles qui se forment sont semblables entre eux, ou comprendre comment passer de 125 à 100 et trouver le rapport 4/5) et calculer progressivement les longueurs des différents segments en tenant compte que chaque longueur s'obtient en multipliant la précédente par le rapport constant 4/5 soit par 0,8, donc après 125 et 100 on obtient : 80 ; 64 ; 51.2 ; 40,96 ; 32,768 ; 26,214 ; 20,972, 16,777; 13,422 ; 10,737 ; 8,590 ; 6,872 ; 5 498…(en cm).

Comprendere quindi che la procedura di addizione può continuare all’infinito ma che gli addendi diventano sempre più piccoli e quindi che la somma cresce sempre meno. Decidere allora a che punto fermarsi, tenendo conto delle dimensioni della formichina o del proprio disegno. Per esempio, se ci si ferma al 15º addendo (che, con il disegno corrisponde al segmento che è possibile tracciare ancora in modo chiaro) si ottiene circa 603. Tale procedura consente di trovare “solo” un’approssimazione della lunghezza del percorso. Per esempio, la somma dei valori precedenti porta a 603,009..

- È anche possibile una procedura con le misure dei segmenti su un disegno, purché tale disegno sia preciso e in scala. Il primo triangolo rettangolo avrà i lati, per esempio, espressi in mm, di lunghezze rispettive 125, 100 e 75 (con il teorema di Pitagora). In questo caso, leggendo le misure approssimate al mm, si arriva a circa 610 mm da 16 a 17 segmenti.

Oppure, con conoscenze relative alla somma di una progressione geometrica, eventualmente acquisite a livello della categoria 10, con il ricorso al rapporto tra le lunghezze dei segmenti, considerare la somma della progressione, tenendo conto “intuitivamente” che i termini tendono a 0

S = 125 + 125(4/5) + 125(4 /5)$^2$ +…

Moltiplicando poi ambo i membri per 4/5: (4/5) S = 125 (4/5) + 125 (4/5)$^2$ +… e scrivendo la differenza fra le due relazioni si ottiene: S - (4/5) S = 125 e infine S = 625

Oppure, considerando la configurazione geometrica della spezzata, con le due successioni di segmenti tra loro paralleli:

impostare la proporzione tra il rapporto della lunghezza S della spezzata e la lunghezza del primo segmento e il rapporto della lunghezza della spezzata meno il primo segmento e il secondo segmento: S/125 = (S-125)/100, che conduce a S = 625 (in cm) (procedura che potrebbe essere considerata come una generalizzazione della similitudine).

//In vista di una possibile attività in classe successiva alla prova, potrebbe essere interessante “costruire” con gli allievi il secondo e il terzo procedimento per arrivare anche a osservare che, in questi due casi, si ottiene l’effettiva lunghezza della spezzata, mentre con il primo ci si avvicina sempre di più, ma il processo “non finisce”!

Nozioni matematiche

progression géométrique, similitude, rapport, raison, limite, approximations, idée d’infini, convergence d’une série, Thales

Risultati

30.I.19

sur 363 classes de 10 sections

Categoria	0	1	2	3	4	Nb.classi	Media
Cat 9	30 (17%)	26 (15%)	97 (55%)	17 (10%)	5 (3%)	175	1.66
Cat 10	25 (13%)	27 (14%)	113 (60%)	10 (5%)	13 (7%)	188	1.78
Totale	55 (15%)	53 (15%)	210 (58%)	27 (7%)	18 (5%)	363	1.72
Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema.

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Risposte corrette (disegno che tenga conto della perpendicolarità richiesta e accenno alla “impossibilità a completarlo” come suggerito dall’enunciato e dalla domanda; con percorso che arrivi fino ad almeno il 14$^o$ o 15$^o$ segmento e lunghezza della spezzata che superi i 600 cm, o inferiore a 625 cm) con dettaglio dei calcoli sia con l’individuazione del rapporto sia con le misure con un disegno in scala
• 3 points: Risposte corrette con dettaglio dei calcoli non completo
  oppure disegno corretto fino ad almeno il 12$^o$ o il 13$^o$ segmento e lunghezza della spezzata compresa tra 580 cm e 600 cm, con dettaglio dei calcoli
• 2 points: Risposte corrette, senza dettaglio dei calcoli
  oppure disegno corretto fino almeno al 10$^o$ o 11$^o$ segmento e lunghezza come somma di lunghezze dei segmenti trovati con un errore di calcolo o di misurazione che si desume dal dettaglio presentato
  oppure disegno corretto fino ad almeno il 12o o il 13o segmento e lunghezza ottenuta con un calcolo o delle misure coerenti
• 1 point: Inizio di ragionamento corretto (disegno con almeno sei segmenti o calcolo delle lunghezze ma non viene fatta la somma, …)
  oppure individuazione della lunghezza del terzo segmento con rapporto corretto
  oppure risposta del tipo: poiché gli addendi sono infiniti, la lunghezza è infinita, con almeno un inizio corretto di disegno
• 0 point: Incompréhension du problème

Per andare più lontano

Grugnetti L., Rizza A. con il contributo di Federica Curreli e Cinzia Utzeri. (2024). PROBLEMA “A ZIG ZAG”/PROBLÈME « Á ZIG ZAG » In Gazette de Transalpie / Gazzetta del Translpino 14 pp 47-60