Deux fourmis en promenade

Identification

Rallye: 31.I.17 ; catégories: 8, 9, 10 ; domaines: GP, GM
Familles:

• GDE - Organiser une suite de relations en géométrie déductive
• LA - Utiliser des mesures de longueurs et aires
• RD - Rechercher ou utiliser des dimensions

Envoyer une remarque ou une suggestion

Résumé

Calculer des distances sur un pavage composé d'hexagones réguliers entourés de six carrée et six triangles équilatéraux

Enoncé

Tâche de résolution et savoirs mobilisés

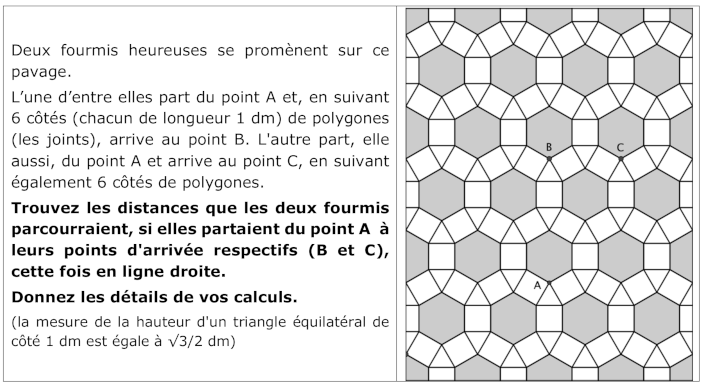
Appropriation

Vérifier les parcours décrits par l'énoncé en suivant 6 côtés et comprendre que la distance en ligne droite du point A au point B doit être calculée sur le segment constitué d'une diagonale de l'hexagone de sommet A, de la hauteur de deux triangles équilatéraux et d'un axe de symétrie parallèle à deux côtés d'un carré, qui se trouvent entre A et B ; tandis que la distance entre A et C doit être calculée sur le segment constitué de deux cordes respectivement des deux hexagones impliqués et de deux côtés respectivement de deux triangles impliqués.

Savoirs mobilisés

Savoir qu'un hexagone hexagone régulier peut se décomposer en six triangles équilatéraux, ses diagonales sont composées de 2 côtés de ses triangles et la distance entre deux côtés parallèles correspond à deux hauteurs de ses triangles. Comme la mesure de la hauteur d'un triangle équilatéral de côté 1 est donnée dans l'énoncé, la hauteur d'un triangle équilatéral de côté 1 dm est égale à √3/2 dm il faut savoir appliquer cette donnée ou de la recalculer en se référant à la relation de Pythagore: comprendre les notations √3, et √3/2 ou en donner une approximation "raisonnable", ...)

Procédures

Tracer les deux segments de droite représentant les distances de A à B et de A à C et les décomposer en côtés de mesure 1 (dm) ou de hauteurs de triangles équilatéraux dont chaque hexagones.

- La distance AB, est composée de la longueur d'une diagonale de l'hexagone (ou de deux côtés de triangle), 2 dm, la longueur du côté d’un carré (1 dm) et deux fois la hauteur d'un triangle, (√3/2 dm), c’est-à-dire 3 + √3 en dm ou par une approximation ≈ 4,73

- La distance AC, est composée de 4 hauteurs de triangles contenus dans deux hexagone et de deux côtés de trianglesc'est-à-dire 4(√3/2) + 2 = 2√3 + 2 ≈ 5,46.

Il est aussi possible de trouver des approximations de ces deux distances sur un dessin précis, à l'échelle.

Notions mathématiques

triangle équilatéral, hexagone, carré, relation de Pythagore, angle, pavage

Résultats

31.I.17

Points attribués, sur 1216 classes de 20 sections:

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Les deux réponses correctes, (en dm, AB = (3 + √3) et AC = 2(√3 + 1) ou deux valeurs approximatives (en dm, ≈ 4,73 et ≈ 5,46, avec les symboles d’approximation ou « environ » avec les détails des calculs
• 3 points: Les deux réponses correctes sans les détails des calculs pour une des deux distances
• 2 points: Les deux réponses correctes sans les détails des calculs
  ou la première réponse erronée à cause d’un calcul erroné et deuxième réponse correcte avec les détails
  ou une seule distance correcte, mais avec les détails des calculs
  ou les deux réponses (4,73 et 5,46 (en dm) sans les symboles d’approximation ou sans « environ » mais avec le détail des calculs
• Une réponse correcte sans détails des calculs
  ou début de raisonnement correct pour les deux distances
  ou les deux réponses avec mesures directes sur une figure et transformation en décimètres (environ 4 ou 5 et 5 ou 6 respectivement)
• 0 point: Incompréhension du problème

Procédures, obstacles et erreurs relevés

Analyses a posteriori en cours. Il s'agira de déterminer les raisons de l'échec du problème en catégorie 8 et du dem-échec en catégories 9 et 10.