Due formiche a passeggio

Identificazione

Rally: 31.I.17 ; categorie: 8, 9, 10 ; ambiti: GP, GM
Famiglie:

• GDE - Organizzare una successione di relazioni in geometria deduttiva
• LA - Utilizzare misure di lunghezze e aree
• RD - Ricercare o utilizzare dimensioni

Envoyer une remarque ou une suggestion

Sunto

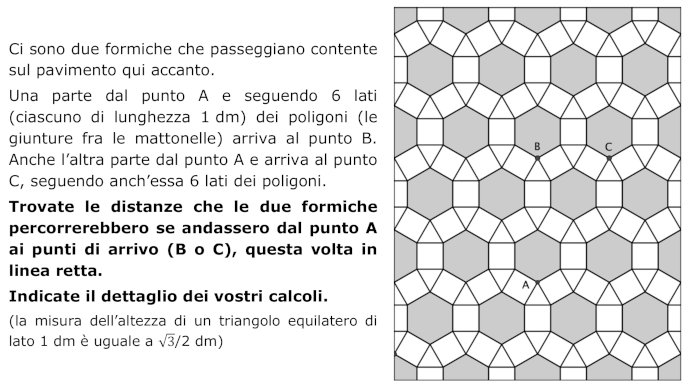
Calcolo di distanze a partire dalla misura del lato di un esagono regolare.

Enunciato

Compito per la risoluzione e saperi mobilizzati

Appropriazione

Controllare i percorsi descritti nell'enunciato seguendo 6 lati e comprendere che la distanza in linea retta dal punto A al punto B deve essere calcolata sul segmento costituito da una diagonale dell'esagono con vertice A, l'altezza di due triangoli equilateri e un asse di simmetria parallelo a due lati di un quadrato, che si trovano tra A e B; mentre la distanza tra A e C deve essere calcolata sul segmento costituito rispettivamente da due corde dei due esagoni coinvolti e rispettivamente da due lati dei due triangoli coinvolti.

Saperi mobilitati

Sapere che un esagono regolare può essere scomposto in sei triangoli equilateri, le sue diagonali sono composte da due lati di questi triangoli e la distanza tra due lati paralleli corrisponde a due altezze di questi triangoli. Poiché l'altezza di un triangolo equilatero con lato di lunghezza 1 è data nell'enunciato del problema, l'altezza di un triangolo equilatero con lato di lunghezza 1 dm è uguale a √3/2 dm, è necessario essere in grado di applicare questa informazione o di ricalcolarla utilizzando il teorema di Pitagora: comprendere le notazioni √3 e √3/2, o fornire un'approssimazione "ragionevole", ecc.

Procedure

Disegnare i due segmenti che rappresentano le distanze da A a B e da A a C e scomponile in lati di lunghezza 1 (dm) o altezze di triangoli equilateri, ciascuno contenente un esagono.

- La distanza AB è composta dalla lunghezza di una diagonale dell'esagono (o di due lati di un triangolo), 2 dm, dalla lunghezza di un lato di un quadrato (1 dm) e dal doppio dell'altezza di un triangolo, (√3/2 dm), ovvero 3 + √3 in dm, o per approssimazione ≈ 4,73.

- La distanza AC è composta da 4 altezze di triangoli contenuti in due esagoni e due lati di triangoli, ovvero 4(√3/2) + 2 = 2√3 + 2 ≈ 5,46.

È anche possibile trovare approssimazioni di queste due distanze su un disegno in scala preciso.

Nozioni matematiche

triangolo equilatero, esagono, quadrato, teorema di Pitagora, angolo, pavimentazione

Risultati

31.I.17

Punteggi attribuiti, su 1216 classi di 20 sezioni:

Secondo i criteri dell’analisi a priori :

• 4 punti: Le due risposte corrette “AB = 3 + √3 (in dm) e AC = 2 (√3 + 1) (in dm) o i due valori approssimati $\approx$ 4,73 e $\approx$ 5,46 (in dm) (con il simbolo $\approx$ o con il termine “circa”) e con i dettagli dei calcoli
• 3 punti: Le due risposte corrette senza i dettagli dei calcoli per una delle due distanze
• 2 punti: Le due risposte corrette, ma senza i dettagli dei calcoli
  oppure la prima risposta errata per un calcolo errato e seconda risposta corretta con dettagli
  oppure una sola distanza corretta, ma con i dettagli dei calcoli
  oppure le due risposte 4,73 e 5,46 (in dm) senza il “circa”, ma con dettaglio dei calcoli
• 1 Una risposta corretta senza dettagli dei calcoli
  oppure inizio corretto di ragionamento per entrambe le distanze
  oppure entrambe le risposte con misura diretta sulla figura e trasformazione in decimetri (circa 4 o 5 e 5 o 6 rispettivamente)
• 0 punto: Incomprensione del problema oppure solo risposta con misura sulla figura

Procedure, ostacoli ed errori rilevati

Sono in corso analisi a posteriori. L'obiettivo sarà di determinare le ragioni del fallimento del problema nella categoria 8 e del fallimento parziale nelle categorie 9 e 10.