Le terrain à diviser

Identification

Rallye: 31.I.13 ; catégories: 7, 8 ; domaines: GP, GM
Familles:

• CA - Comparer des aires
• CA/P - Comparer des aires sur un quadrillage
• LA - Utiliser des mesures de longueurs et aires
• RD - Rechercher ou utiliser des dimensions
• RD/AP - Déterminer des aires et/ou périmètres

Envoyer une remarque ou une suggestion

Résumé

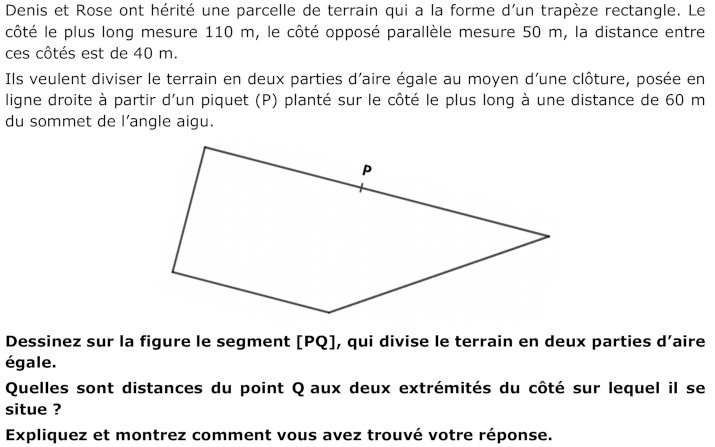
Diviser un trapèze rectangle en deux parties de même aire au moyen d'un segment ayant une extrémité en un point de sur la grande base et l'autre extrémité à déterminer sur l’un des autres côtés du trapèze.

Enoncé

Tâche de résolution et savoirs mobilisés

Analyse de la tâche a priori

- Repérer les angles droits et l’angle aigu du trapèze et associer les bonnes mesures aux différents segments qui forment la figure et observer que le point P, qui est à 60 m du sommet de l'angle aigu, est à 50 m de l'autre extrémité du côté le plus long.

- Calculer l'aire du trapèze (3200 m$^2$) puis en déduire l'aire de chacune des deux parties soit 1600 m$^2$.

- Réaliser éventuellement que si le point Q était sur le côté de 40 m, ou sur le côté non parallèle aux deux bases, l’une des deux figures obtenues serait un triangle de surface trop petite, n'ayant pas une aire de 1600 m$^2$.

En déduire (ou imaginer d’abord) que point Q est sur la petite base.

Observer maintenant que le segment [PQ] divise le trapèze d'origine en un trapèze rectangle et un autre trapèze non rectangle.

Si l'on considère le trapèze rectangle, sachant que la surface est de 1600 m$^2$, que la hauteur est de 40 m et la base de 50 m, afin de trouver l'autre base et donc la position du point Q, on peut procéder :

- par essais successifs

- en utilisant la formule inverse de l’aire du trapèze pour obtenir que (1600 × 2 ÷ 40) = 80 qui donne la somme des bases, et sachant alors que l'une des deux bases mesure 50 m, comprendre que l'autre doit mesurer 30 m.

Ou bien

- Reconstituer un rectangle à partir du trapèze proposé puis partager ce rectangle en 2 trapèzes de même aire, symétriques l’un de l’autre par rapport au centre du rectangle obtenu.

Notions mathématiques

rectangle, trapèze rectangle, carré, triangle, partage, aire, segment

Résultats

31.I.13

Points attribués, sur 2074 classes de 20 sections:

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Réponse correcte « dessin du segment PQ, Q sur la petite base et les deux distances notées : 30 m et 20 m à gauche et à droite de Q », avec des explications claires et complètes de la procédure utilisée
• 3 points: Réponse correcte, avec des explications peu claires
• 2 points: Réponse correcte, sans aucune explication
  ou réponse qui indique une procédure correcte mais avec des erreurs de calculs
• 1 point: Début correct de la recherche avec le calcul de la superficie du terrain et des deux parties dans lesquelles la hauteur divise le trapèze
• 0 point: Incompréhension du problème

Procédures, obstacles et erreurs relevés

Analyse a posteriori en cours