Il terreno da dividere

Identificazione

Rally: 31.I.13 ; categorie: 7, 8 ; ambiti: GP, GM
Famiglie:

• CA - Comparer des aires
• CA/P - Comparer des aires sur un quadrillage
• LA - Utiliser des mesures de longueurs et aires
• RD - Rechercher ou utiliser des dimensions
• RD/AP - Déterminer des aires et/ou périmètres

Envoyer une remarque ou une suggestion

Sunto

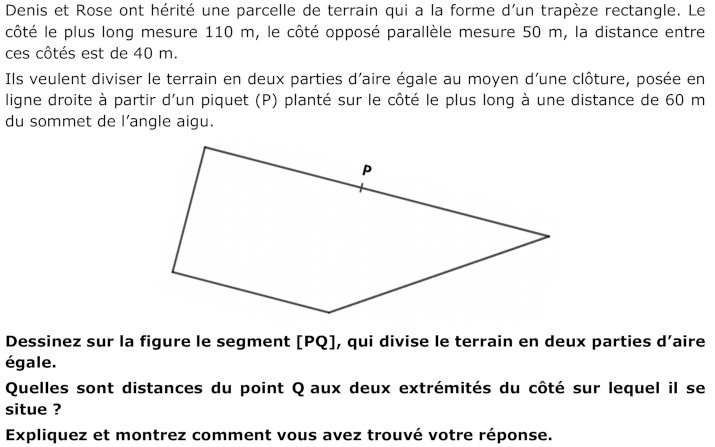
Ripartire un trapezio rettangolo in due parti della stessa area mediante un segmento avente un estremo in un punto della base maggiore e l’altro estremo da determinare su uno degli altri lati del trapezio.

Enunciato

Compito per la risoluzione e saperi mobilizzati

Analisi del compito a priori

- Individuare gli angoli retti e l’angolo acuto del trapezio e associare le “buone misure” ai diversi lati della figura e osservare che il punto P, che si trova a 60 m dal vertice all’angolo acuto, deve trovarsi a 50 m dall’altro estremo del lato lungo.

- Calcolare l’area del trapezio (3200 m$^2$) e dedurre che l’area di ciascuna parte è 1600 m$^2$.

- Immaginare eventualmente che il punto Q si trovi sul lato di 40 m, o sul lato non parallelo alle due basi: una delle due figure ottenute sarebbe un triangolo di area troppo piccola, inferiore a 1600 m$^2$.

- Dedurre (o immaginare dapprima) che il punto Q si trova sulla base minore. A questo punto osservare che il segmento PQ divide il trapezio originale in un trapezio rettangolo e in un altro trapezio non rettangolo.

- Se si considera il trapezio rettangolo, sapendo che l’area è di 1600 m$^2$., che l’altezza è di 40 m e la base di 50 m per arrivare a trovare l’altra base e quindi la posizione del punto Q, si può procedere:

- per tentativi successivi

- tramite la formula inversa del trapezio (1600 × 2 ÷ 40) = 80 che dà la somma delle basi e poi sapendo che una delle due basi misura 50 m capire che l’altra deve misurare 30 m.

oppure

- Costruire un rettangolo a partire dal trapezio proposto, poi dividere questo rettangolo in due trapezi aventi la stessa area, simmetrici rispetto al centro del rettangolo ottenuto

Nozioni matematiche

rettangolo, trapezio rettangolo, quadrato, triangolo, divisione, area, segmento

Risultati

31.I.13

Punteggi attribuiti, su 2074 classi d1 20 sezioni:

Secondo i criteri determinarti dall’analisi a priori :

• 4 points: Risposta corretta “disegno del segmento PQ, Q sulla base minore, con l’indicazione delle due distanze: 30 m et 20 m a sinistra e a destra di Q”, con spiegazioni chiare e complete della procedura utilizzata
• 3 points: Risposta corretta con spiegazioni poco chiare
• 2 points: Risposta corretta senza alcuna spiegazione
  oppure risposta che indica una procedura corretta ma con errori di calcolo
• 1 point: Inizio corretto di ricerca con il calcolo dell’area del terreno e delle due parti in cui l’altezza divide il trapezio
• 0 point: Incomprensione del problema

Procedure, ostacoli ed errori rilevati

Analisi a pasteriori in corso