Girouette de triangles

Identification

Rallye: 31.I.16 ; catégories: 7, 8, 9, 10 ; domaine: GP
Familles:

• CA - Comparer des aires
• DEC - Découper et/ou assembler des figures

Envoyer une remarque ou une suggestion

Résumé

A partir de l'image de quatre triangles rectangles identiques, par des déplacements judicieux des pièces, trouver l'aire exacte d'un triangle dont on connaît la longueur de l'hypoténuse (7 cm) et la différence de longueur entre les côtés de l’angle droit (1 cm).

Enoncé

Tâche de résolution et savoirs mobilisés

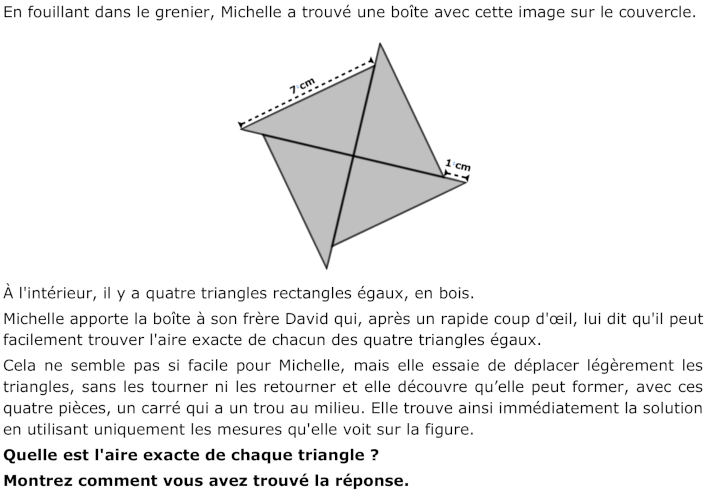
- Comprendre la situation : les quatre triangles sont rectangles et tous identiques, ils ont une hypoténuse de 7 cm de long et un côté de l’angle droit plus long de 1 cm que l'autre côté de l’angle droit, il faut construire un carré avec un "trou" avec tous les triangles, il faut trouver l'aire d'un triangle.

- En découpant et en composant les triangles ou en dessinant, essayer de construire le carré et réaliser qu’il est possible de le faire en laissant un carré vide de 1 cm de côté au centre.

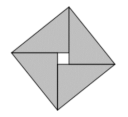
- Trouver l'aire du carré construit (7 × 7 = 49) (en cm$^2$) et retirer l'aire du carré vide (1 × 1 = 1) (en cm$^2$) pour trouver l'aire totale des quatre triangles (49 – 1 = 48) (en cm$^2$). Puisque les triangles sont tous identiques, il suffit de diviser l'aire totale par 4 pour trouver l'aire d'un triangle (48 ÷ 4 = 12 (en cm$^2$)

- Ou, par voie algébrique, indiquer par x et x + 1 les mesures dei côtés de l’angle droit et résoudre l’équation x$^2$ + (x + 1)2 = 49 et calculer l’aire du triangle par substitution des valeurs obtenues dans la formule x(x + 1) : 2.

Notions mathématiques

carré, triangle, triangle rectangle, aire, longueur, mesure de longueur, déduction, équivalence, décomposition, similitude, rapport, isométrie, translation, rotation

Résultats

31.I.16

sur 2461 classes de 20 sections

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Réponse correcte « aire du triangle = 12 cm$^2$ », sans aucune approximation, avec description claire et complète (reconstruction, même peu précise, du carré, détails et explication des calculs)
• 3 points: Réponse correcte, sans aucune approximation avec une description peu claire ou incomplète
  ou réponse entre 11,88 cm$^2$ et 12,38 cm$^2$ ou 12,375 cm$^2$ du fait d'une approximation, avec une description claire et complète (détails et justification des calculs)
  ou réponse 48 (oubli de la division par 4) avec description claire et complète
• 2 points: Réponse correcte sans description
  ou réponse entre 11,88 cm$^2$ et 12,38 cm$^2$ ou 12,375 cm$^2$ due à une approximation, avec description peu claire ou incomplète (calculs incomplets ou non justifiés)
• 1 point: Début de raisonnement correct, par exemple pour trouver l'aire du carré de côté 7 cm
  ou mauvaise réponse : 12,25 cm$^2$ (49 cm$^2$ ÷ 4) et oubli d'enlever le centimètre carré central
• 0 point: Incompréhension du problème