Con quattro triangoli

Identificazione

Rally: 31.II.07 ; categorie: 5, 6, 7 ; ambiti: GP, GM
Famiglie:

• LA - Utilizzare misure di lunghezze e aree
• RD - Ricercare o utilizzare dimensioni
• RD/AP - Determinare aree e/o perimetri

Envoyer une remarque ou une suggestion

Sunto

Costruire un poligono di perimetro massimo assemblando quattro triangoli ottenuti dalla scomposizione di un quadrato di lato 10 cm.

Enunciato

Compito per la risoluzione e saperi mobilizzati

Analisi del compito a priori:

Appropriazione: osservare la figura e rendersi conto che i due triangoli grigi sono rettangoli, i due triangoli bianchi sono isosceli (il più piccolo è rettangolo isoscele). Capire che i lati possono essere di quattro lunghezze diverse: i cateti minori dei triangoli rettangoli, i cateti maggiori dei triangoli rettangoli grigi (che sono il doppio del cateto minore), le ipotenuse dei triangoli grigi e l’ipotenusa del triangolo rettangolo isoscele. (Nel caso si volessero calcolare i perimetri, le misure dei lati sono 5 cm, 10 cm, circa 7 cm e circa 11 cm).

Procedure per questo tipo di “puzzle”:

A. Disegno del quadrato di 10 cm di lato, poi ritaglio dei quattro triangoli e ricerca di composizioni fino a stimare quale è la figura di perimetro più lungo. Si possono ottenere otto possibili diversi perimetri: tra 64 e 65 m il maggiore, poi tra 56 e 57 cm il seguente, poi tra 54 e 55 cm, tra 52 e 53 cm, tra 46 e 47, circa 44 cm, circa 42 cm e infine 40 cm per il perimetro minore (quello del quadrato).

B. Disegno delle figure (per esempio su carta quadrettata) per fare un esempio di figura per ogni possibile perimetro.

C. Per ricerca di composizioni in cui i lati più corti dei triangoli sono “all’interno” della figura e i lati più lunghi sono sul contorno della figura. La spiegazione del perimetro massimo è legata alla procedura C ma può anche derivare dalle procedure A e B per mezzo di diversi tentativi che portino progressivamente all’elenco dei diversi possibili perimetri.

Le tre figure di perimetro massimo (tra 64 e 65 cm) sono quelle in Figura 5.

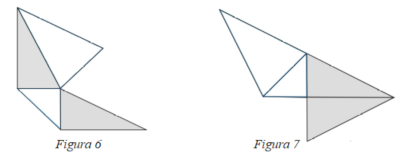
- Un esempio di figura di perimetro tra 56 e 57 cm (il secondo in ordine di grandezza) è quella in Figura 6.

- Un esempio di figura di perimetro tra 54 e 55 cm (il terzo in ordine di grandezza) è quella in Figura 7.

Nozioni matematiche

poligono, triangolo, triangolo rettangolo, composizione, perimetro, lunghezza, lato, addizione, massimo

Risultati

31.II.07

Points attribués sur 3321 classes de 20 sections:

Selon les critères déterminés lors de l’analyse a priori :

• 4 punti: Disegno di una delle tre figure possibili di perimetro massimo (Fig.5), con calcolo del perimetro (tra 64 e 65 cm) o con spiegazione del perché il perimetro è massimo (per esempio i lati più lunghi “all’esterno”, i più corti “all’interno”)
• 3 punti: Disegno di una delle tre figure possibili di perimetro massimo (Fig.5), con calcolo del perimetro (tra 64 e 65 cm), senza spiegazione del perché il perimetro è massimo
  oppure disegno di una figura possibile con il secondo perimetro più lungo (tra 56 e 57 cm) (per es. Fig 6 o figure isoperimetriche) con spiegazione
• 2 punti: Disegno di una delle figure possibili con il terzo perimetro più lungo (tra 54 e 55 cm) (per es. Fig 7 o figure isoperimetriche) con o senza spiegazione
• 1 punto: Disegno di figure con perimetro inferiore delle precedenti
• 0 punto: Incomprensione del problema.

Procedure, ostacoli ed errori rilevati

È l'analisi degli elaborati con "0 punti" (quasi la metà) che ci permetterà di capire dove risiedono gli ostacoli in questo problema: leggere l'enunciato del problema e comprendere la regola per giustapporre i triangoli? Difficoltà nell'esprimere le misure dei lati irrazionali usando approssimazioni (5√2 diviso 7,1; 5√5 diviso 8,7)? ...

Bibliografia

Bisso C. Grugnetti L. Gruppo geometrie piana (2024). Geometria piana nell'ARMT / La géometrie plane dans l’ARMT. In Gazzzetta del Transalpino/ Gazette de Transalpie no 15 pp 141 - 155