ARMT

Banca di problemi del RMT

gp197-it

 centre

Giardino geometrico

Identificazione

Rally: 31.II.18 ; categorie: 9, 10 ; ambito: GM
Famiglie:

Envoyer une remarque ou une suggestion

Sunto

Trovare la lunghezza di un sentiero deducendola da quella di un altro sentiero, con l’aiuto di considerazioni geometriche basate sulla congruenza di triangoli rettangoli e sul teorema di Pitagora.

Enunciato

Compito per la risoluzione e saperi mobilizzati

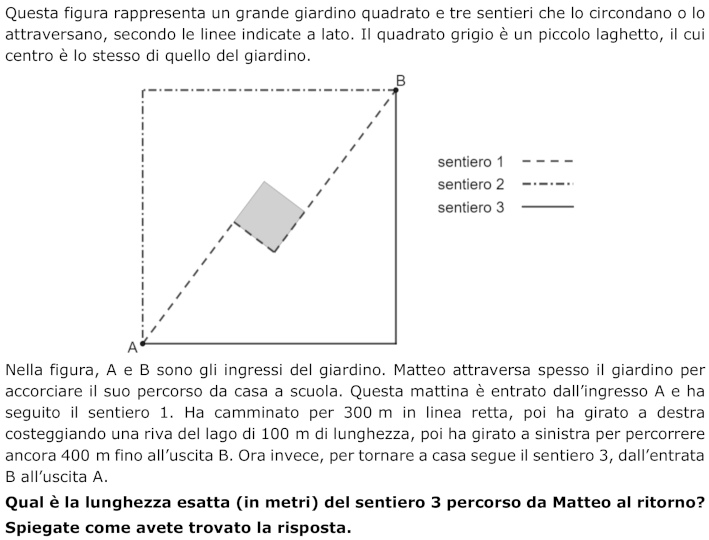
- Appropriarsi della situazione: capire che una volta conosciuta la lunghezza del percorso AEFGB (sentiero 1), bisogna trovare la lunghezza del percorso ADB, sentiero 3.


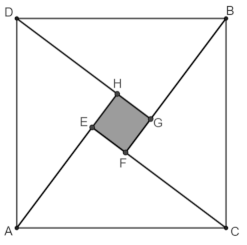
- Considerare i quattro triangoli ACE, CBF, BGD, DHA e riconoscere che sono triangoli rettangoli congruenti perché hanno le ipotenuse e gli angoli adiacenti all’ipotenusa congruenti (per esempio BĈF = EÂC perché sono entrambi complementari di FĈA, FĈA = FBC perché entrambi complementari di FĈB, idem per tutte le altre coppie di triangoli considerate).

- Dedurre le misure dei lati dei triangoli: AE = CF = BG = DH = 300 m; CE = BF = DG = AH = 400m

- Applicare il teorema di Pitagora per ottenere le misure dei lati del quadrato ACBD: AC = CB = BD = DA = 500 m

- Concludere che Matteo, scegliendo il sentiero 3, ha percorso 1000 m.

Nozioni matematiche

geometria, triangolo rettangolo, quadrato, rotazione, ipotenusa, Pitagora, lato

Risultati

31.II.18

Punteggi attribuiti su 382 classi:

Categoria01234Nb.classiMedia
Cat 960 (30%)14 (7%)56 (28%)57 (28%)15 (7%)2021.77
Cat 1046 (26%)23 (13%)34 (19%)57 (32%)20 (11%)1801.9
Totale106 (28%)37 (10%)90 (24%)114 (30%)35 (9%)3821.83
Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema.

Secondo i criteri dell’analisi a priori :

  • 4 points: Risposta corretta “1000 m o 1 km” con procedimento ben spiegato (dimostrazione della congruenza dei triangoli rettangoli e applicazione del Teorema di Pitagora)
  • 3 points: Risposta corretta ma con spiegazione parziale (constatare che i triangoli sono uguali senza dimostrazione o dimostrazione incompleta o poco chiara)
  • 2 points: Risposta corretta senza spiegazioni o solamente con la divisione del disegno in quattro triangoli
  • 1 point: Inizio di ragionamento corretto (per esempio suddivisione del disegno in quattro triangoli o misure prese sul disegno e non reali)
  • 0 point: Incomprensione del problema

Procedure, ostacoli ed errori rilevati

problema ispirato da Passegiata nel parco (18.I.18)