Il quadrato di Paolo

Identificazione

Rally: 31.F.18 ; categorie: 9, 10 ; ambiti: GP, GM
Famiglie:

• RD - Ricercare o utilizzare dimensioni
• RD/AP - Determinare aree e/o perimetri

Envoyer une remarque ou une suggestion

Sunto

A partire da un quadrato di lato assegnato, calcolare l’area di ciascuna delle parti in cui il quadrato viene diviso da due segmenti perpendicolari tra loro.

Enunciato

Compito per la risoluzione e saperi mobilizzati

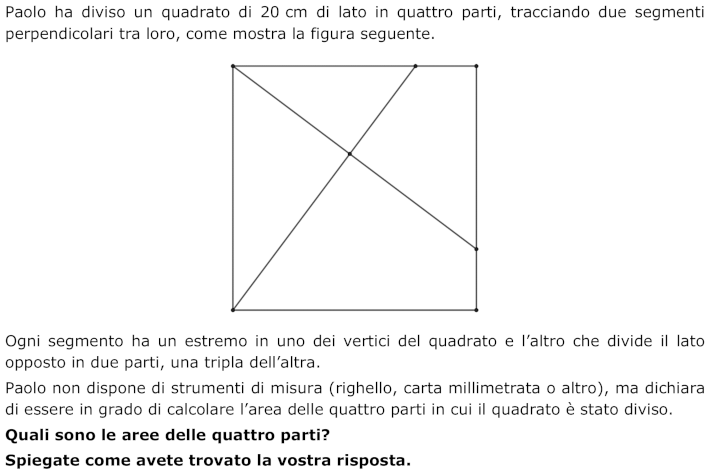
Appropriazione Osservare la figura dell'enunciato, notare che molti segmenti hanno lunghezze di 5, 15 e 20 cm sui lati del quadrato, che i tre triangoli rettangoli (quello piccolo in alto, quello medio a sinistra e quello grande composto dagli altri due) sono simili e che le loro rispettive ipotenuse misurano 15, 20 e 25 cm (Pitagora: lati dell'angolo retto 15 e 20).

Saperi Teorema di Pitagora, conservazione delle misure degli angoli con una rotazione di 90 gradi, proporzionalità tra le lunghezze dei lati di triangoli simili.

Soluzione Per coloro che hanno compreso la proporzionalità tra i rispettivi lati dei tre triangoli in alto a sinistra della figura e hanno calcolato la lunghezza dell'ipotenusa del triangolo maggiore, è sufficiente completare le tre terzine in cm: 15, 20, 25 per il triangolo maggiore, ..., ..., 20 per il triangolo medio, ..., ..., 15 per il triangolo minore utilizzando i rapporti 25/20 = 5/4 (grande/medio), 25/15 = 5/3 (grande/piccolo). Le lunghezze dei lati (in cm) del triangolo medio sono 12, 16 e 20, e 9, 12 e 15 per il triangolo minore.

Le aree sono, in cm², (9 x 12)/2 = 54 per il triangolo piccolo (in alto), (12 x 16)/2 = 96 per il triangolo centrale (a sinistra), 150 - 54 = 96 per il quadrilatero destro e 400 - 96 - 96 - 54 = 154 per il quadrilatero inferiore.

Analisi a priori d'origine, utilizzando la notazione "tradizionale"; la domanda è se questa notazione non sia un "ostacolo"?

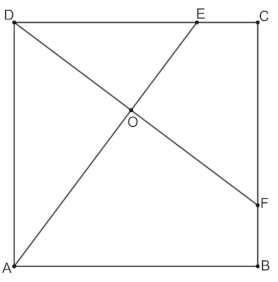
- Applicare l’uguaglianza dei rapporti di similitudine: AO/AD = AD/AE = 20/25 = 4/5, DO/DA = DE/AE = 15/25 = 3/5. - Da cui le misure dei lati (in cm): AO = 20×4/5 = 16 e DO = 20×3/5 = 12. Inoltre, OE = 25 – 16 = 9. Oppure - Calcolare la misura dell’altezza del triangolo DAE relativa alla base AE: DO = (20 x 15 )/25 = 12 (in cm). Calcolare le misure dei segmenti AO, OE tramite il teorema di Pitagora e/o di Euclide, per esempio: OE = √15! − 12! =√81 = 9 (in cm) e AO = √20! − 12! =√256 =16 (in cm). Dedurre le misure delle aree richieste (in cm2): area (DAO) = (16´12)/2 = 96; area (DOE) = (12´9)/2 = 54; area (EOFC) = area (DFC) – area (DOE) = (20´15)/2 – 54 = 96; area (ABFO) = area (ABCD) – area (DAO) – area (DOE) – area (EOFC) = 400 – 96 – 54 – 96 = 154.

le carré de Joseph (19.F.16)

Nozioni matematiche

triangolo, poligono, isometria, similarità, Pitagora, deduzione, proporzionalità

Risultati

31.F.18

Punteggi attribuiti su 55 classi di 8 sezioni

Secon i criteri dell’analisi a priori :

• 4 points: Risposte corrette (54 cm², 96 cm², 96 cm², 154 cm²) con la descrizione chiara della procedura seguita e dettaglio dei calcoli
• 3 points: Risposte corrette con spiegazioni poco chiare
  oppure determinate correttamente tre aree con spiegazioni chiare senza il calcolo dell’area della quarta parte
  oppure risposta completa con un solo errore di calcolo con spiegazioni chiare
• 2 points: Risposte corrette senza spiegazioni
  oppure due aree corrette e due aree errate a causa di errori di calcolo ma con spiegazioni chiare
• 1 point: Inizio di ragionamento coerente
• 0 point: Incomprensione del problema

Indicazioni didattiche

La situazione è interessante perché presenta tre triangoli rettangoli simili (in alto a sinistra) ben noti, le cui misure dei lati sono proporzionali a 3, 4 e 5. Tagliandoli e spostandoli, è possibile sovrapporli con un vertice in comune e lati paralleli corrispondenti, immagini l'uno dell'altro per omotetie, che sono visivamente più facili da osservare rispetto alle somiglianze.