Il trapezio del prof. De Calcolis

Identificazione

Rally: 31.F.19 ; categorie: 9, 10 ; ambiti: GP, GM
Famiglie:

• GDE - Organizzare una successione di relazioni in geometria deduttiva
• IF - Identificare figure
• IF/RC - Riconoscere e costruire figure elementari

Envoyer une remarque ou une suggestion

Sunto

Rappresentare una determinata figura geometrica, analizzarla, riconoscere un’affermazione errata e giustificarla con proprietà geometriche.

Enunciato

Compito per la risoluzione e saperi mobilizzati

Analisi a priori del copito

- Rappresentare un trapezio rettangolo, tagliato lungo la diagonale minore, a partire dalle informazioni corrette sul triangolo di Morgana; il triangolo potrebbe essere messo in due diverse posizioni:

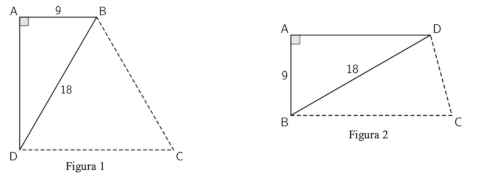
- Constatare che l’affermazione 1 di Valentino non può essere errata perché, se fosse errata, porterebbe automaticamente al fatto che anche l’affermazione 3 sarebbe errata (c'è già un lato che misura 18 cm secondo l'affermazione 3 di Morgana). Dedurre che ci sono almeno due lati congruenti e che il triangolo BDC di Valentino è isoscele.

- Osservare che il triangolo di Morgana deve essere la metà di un triangolo equilatero e quindi con gli angoli di 30° (di vertice D) e 60° (di vertice B).

- Nel primo caso (figura 1) dedurre che l’angolo BDC misura 60° (complementare di 30°).

- Quindi il triangolo BDC è isoscele con un angolo di 60°; se ne deduce che è un triangolo equilatero. Poiché un lato misura 18 cm, anche gli altri due misureranno 18 cm, perciò l’affermazione falsa di Valentino è la 2.

- Nel secondo caso (figura 2), poiché il triangolo BCD deve essere isoscele, dovrà avere due lati che misurano 18 cm oppure due lati che misurano 17 cm. La prima possibilità si verifica se la base maggiore BC misura 18 cm (e DC risulta di circa 9,3 cm e non 17); la seconda non si può verificare perché BD diventerebbe la diagonale maggiore. Pertanto, l’affermazione 2 di Valentino è falsa.

Nozioni matematiche

triangolo, poligono, isometria, similitudine, Pythagore, deduzione, proportionnalità

Risultati

31.F.19

Points attribués sur 54 classes de: 8 sections

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Risposta corretta (affermazione 2) con spiegazione completa che prende in esame i due casi
• 3 points: Risposta corretta con spiegazione incompleta poco chiara, con esame di entrambi i casi
• 2 points: Risposta corretta senza spiegazioni, ma almeno un disegno di uno dei due casi
• 1 point: Inizio di ragionamento corretto (per esempio riconosciuto l’angolo di 60° o fatta qualche deduzione coerente)
• 0 point: Incomprensione del problema