I quadrati di Paolo

Identificazione

Rally: 19.I.04 ; categorie: 3, 4, 5 ; ambito: GP

Remarque et suggestion

Sunto

Formare i possibili quadrati affiancando dei pezzi scelti fra quattro tipologie di figure: un quadrato 1x1, un quadrato 2x2, tre rettangoli 1x2 e tre rettangoli 1x3.

Enunciato

Compito per la risoluzione e saperi mobilizzati

Analisi a priori

Percepire, secondo le figure date, le relazioni tra le dimensioni dei quattro tipi di pezzi: (1 x 1), (1 x 2), (1 x 3) e (2 x 2) per poterli giustapporre.

Comprendere che per costruire i quadrati si possono usare solo gli otto pezzi disponibili per ogni costruzione, ma che non è necessario usarli tutti.

Verificare i due esempi di quadrati di un singolo colore (che però usano svariati pezzi).

Cercare di costruire un quadrato di due colori (con due tipi di pezzi) e osservare che esiste una sola possibilità per un quadrato di 3 x 3, con i tre piccoli rettangoli e un rettangolo grande (vedi sotto). (Non si possono usare né il quadratino nero né quello grande bianco perché per completare la costruzione occorrerebbero altri due tipi di pezzi.) Per un quadrato più grande, 4 x 4, occorrerebbero anche più di due tipi di pezzi. )

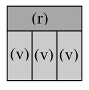
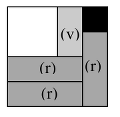
Constatare che per il quadrato con quattro tipi di pezzi, non c'è un quadrato di 3 x 3, per tentativi o considerazioni sulle aree. (I quattro tipi di pezzi danno almeno un'area di 1 + 4 + 2 + 3 = 10, che è maggiore di 3 x 3 = 9). Provando a costruire quadrati di 4 x 4, con i quattro tipi di pezzi, ci si rende conto che esiste una sola soluzione, tramite tentativi (o eventualmente, per gli allievi più grandi, da considerazioni sulle aree: un pezzo di ogni tipo dà già un'area di 10, per andare a 16 è necessario aggiungere due pezzi di area 3, vale a dire due grandi rettangoli.)

Formare quindi un quadrato di 4 x 4 con il piccolo nero, il grande bianco, un piccolo rettangolo verde e i tre grandi rettangoli rossi.

Nozioni matematiche

quadrato, rettangolo, accostamento

Risultati

19.I.04

Punteggi attribuiti su 1539 classi di 20 sezioni:

Secondo i criteri dell’analisi a priori:

• 4 punti: I due quadrati disegnati correttamente con i pezzi ben evidenziati indipendentemente dalla disposizione dei vari pezzi
• 3 punti: I due quadrati disegnati correttamente con l’indicazione dei pezzi, con altri quadrati ottenuti con gli stessi pezzi ma disposte in una maniera diversa (contrariamente alla richiesta: “disegnate un solo quadrato di 2 o 4 colori”)
• 2 punti: Uno dei quadrati con l’indicazione dei pezzi
  oppure i due quadrati disegnati correttamente con uno o più quadrati che non rispettano le condizioni (per esempio due volte il quadrato piccolo o più di tre rettangoli piccoli, oppure tre colori al posto di due)
• 1 punto: Uno o due quadrati di due o quattro colori, che non soddisfano le condizioni
  oppure un rettangolo (non quadrato) che rispetta le condizioni
• 0 punto: Incomprensione del problema

(c) ARMT, 2011-2024