
Banque de problèmes du RMT
gp49-fr
 |
Banque de problèmes du RMTgp49-fr |
|
Envoyer une remarque ou une suggestion

- Comprendre que les "distances" mentionnées dans l'énoncé se mesurent entre deux arbres en "ligne droite" et qu'il s'agira de comparer les longueurs des segments déterminés par deux points sur le dessin.
- Se rendre compte qu'il y a un très grand nombre de distances (segments) entre deux quelconques des 25 points et que beaucoup de ces distances seront égales (segments de même longueur). La plus courte est de 1 (en côté d'un carré de la grille), la plus grande est celle entre deux centres de carrés "opposés" en suivant une diagonale de la grille.
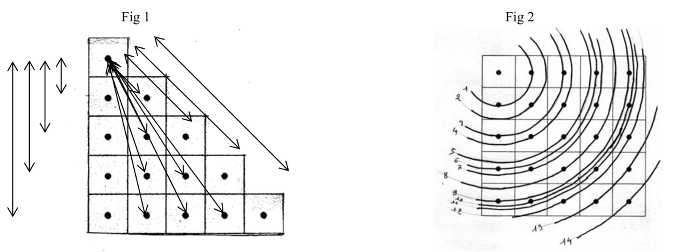
- Comprendre que, pour éviter de compter plusieurs fois une même distance, on peut se limiter aux distances entre un point au centre d'un carré d'un angle (par exemple celui du haut à gauche) et les 24 autres points. Puis, du fait de la symétrie par rapport à une diagonale, on peut encore limiter les comparaisons en ne s'intéressant qu'à 15 points: le point choisi dans un angle et 14 autres, sur et/ou au-dessous de la diagonale.
- Vérifier que du point choisi aux quatre autres de sa colonne il y a 4 distances "verticales" différentes (1, 2, 3, 4) puis que du point choisi aux quatre autres de la colonne voisine il y a encore 4 distances différentes, puis 3 distances différentes avec les 3 points au-dessous de la diagonale de la troisième colonne, puis 2 avec les points de la quatrième colonne et 1 avec le point opposé, (en diagonale), ce qui fait 14 distances. (Fig 1). (Dans le cas particulier de la figure de 25 points (5 x 5), ces 14 distances sont différentes, ce qui ne serait plus le cas dans un "quadrillage" plus grand avec une distance de 5, dans une version plus développée du problème, par exemple avec un "quadrillage" de 6 x 6.)
- Les comparaisons peuvent se faire visuellement, de proche en proche. L'utilisation de la règle graduée n'est nécessaire que pour les deux distances entre le point fixe et, respectivement, celui du bas de la colonne voisine et l'avant dernier en suivant la diagonale. (√17 et √18)
- Une autre manière de déterminer le nombre de distances est l'utilisation du compas (Fig 2)
Sur 276 classes de 5 sections
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 7 | 71 (44%) | 22 (14%) | 38 (24%) | 8 (5%) | 21 (13%) | 160 | 1.29 |
| Cat 8 | 38 (33%) | 19 (16%) | 33 (28%) | 11 (9%) | 15 (13%) | 116 | 1.53 |
| Total | 109 (39%) | 41 (15%) | 71 (26%) | 19 (7%) | 36 (13%) | 276 | 1.39 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
Ce problème a été analysé dans le cadre d'une recherche du "Groupe Géométrie plane pour les grands" sur le concept de distances (voir article en bibliographie, pages 93 à 102) et proposé en particulier dans deux classes de catégorie 7 de Franche-Comté (par f.f).
Un obstacle se situe dans l'appropriation de l'expression "Combien existe-t-il de distances différentes de deux arbres", les élèves pensant souvent à la situation de deux arbres qui se suivent, verticalement ou horizontalement.
Cet obstacle ne permet donc pas d'entrer dans la démarche de recherche des "distances". Lorsqu'il est levé, il faut encore distinguer les distances "différentes" et trouver une procédure qui évite de compter plusieurs fois les mêmes.
Malgré les moyennes basses obtenues dans les conditions de passation de l'épreuve, on se rend compte que la situation proposée par l'énoncé peut être largement exploitée en classe.
Après quelques minutes de recherche individuelle ou par groupes, une mise en commun doit permettre à chacun de s'approprier le tâche: percevoir les "distances"/"longueurs de segments" et éliminer les segments isométriques par le choix d'un point fixe. Si on considère les segments comme des diagonales de rectangles, la comparaison des longueurs de deux segments "voisins" (ou diagonales de deux rectangles de même largeur) se fait par déduction.
La seule comparaison qui nécessite une attention particulière est celle des deux diagonales d'un rectangle (1;4) et du carré (3;3). La différence est visible au compas ou par une construction précise d'un agrandissement de la grille. Elle peut aussi se faire par construction, sur quadrillage de carrés construits sur chacune des diagonales, puis par comptage des carreaux entiers et des parties de carreaux regroupées. Les aires de ces carrés sont respectivement 17 et 18 (en carreaux du quadrillage) et on peut en conclure, par déduction, que les deux segments sont différents. (Même sans Pythagore ni calculs de racines carrées!)
Exemples d'activités en vue d'un parcours didactique avec la classe
À expérimenter en classe, selon des modalités déterminées par l'enseignant; avec envoi de description et commentaires pour rendre compte de l'opportunité de l'activité pour la construction des savoirs (notés en italique).
(On ne peut - ou même on ne doit pas - s’arrêter à la question du "problème de concours" ! Le dénombrement a abouti à la réponse 14 que toute la classe peut admettre après une première mise en commun des résultats. Cependant la discussion ne garantit pas que le concept de « distance » en géométrie a été « construit » ou « reconstruit » ou encore « enrichi » par les élèves. Il reste, pour une majorité d’élèves, au statut de la « distance, visuelle ou dynamique » se rapportant à leurs déplacements, à leurs jeux, à l’éloignement de personnes ou d’objets. L'objet de la proposition qui suit est d'abord la distance.)
Les propositions:
a) Reprendre le même problème, mais avec une "grille) " de 6 x 6 (au moins) au lieu de 5 x 5.
Avec une grille de 6 x 6, on aboutit à 20 distances, dont 19 seulement sont différentes et c'est ici qu'intervient la nécessité d'aller au-delà de la comparaison visuelle pour arriver à une "mesure" des segments correspondants.
Les savoirs: passer du dénombrements de distances différentes entre deux clous à leurs comparaisons, puis à leur mesure, déterminer les relations entre la mesure d’un côté de carré et celle de sa surface (ou aire), découvrir des nombres non entiers et non décimaux et non rationnels, trouver des approximations de nombres que la calculatrice n’est pas en mesure d’afficher précisément.
b) Dessiner quelques carrés dont les côtés sont des distances de l'inventaire. Par exemple, sur la figure suivante:
- le carré construit sur le segment (1 ; 0) ou (0 ; 1) de la deuxième ligne, en haut à gauche,
- le carré construit sur le segmentsur le segment (1 ; 1) de la troisième ligne en haut au milieu,
- le carré construit sur le segmentsur le segment (2 ; 1) ou (1 ; 2) de la cinquième ligne en bas à gauche.
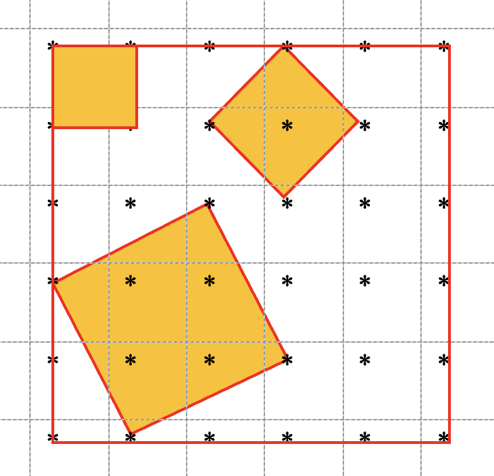
Les savoirs : construction de segments perpendiculaires et isométriques entre deux points d'un quadrillage et perception des relations entre leurs "coordonnées", détermination de l'aire de carrés dont les côtés sont "obliques" à partir de carrés "circonscrits" plus grands dont les côtés sont "horizontaux" et "verticaux", par découpages de quatre triangles isométriques (décomposition et recomposition de figures à deux dimensions).
c) Dresser un inventaire de toutes les distances ou segments entre deux points de la grille. Ces points peuvent être désignés par leurs coordonnées de (0 ; 0) à (5 ; 5) si l'on choisit le point d'une case d'un angle de la grille comme origine des coordonnées (par exemple le centre de la case en haut à gauche des figures 1 et 2).
(Voici un modèle de cet inventaire, sous forme d'un tableau, à compléter avec indications de l'enseignant et débat collectif pour les premières lignes, puis individuellement.)
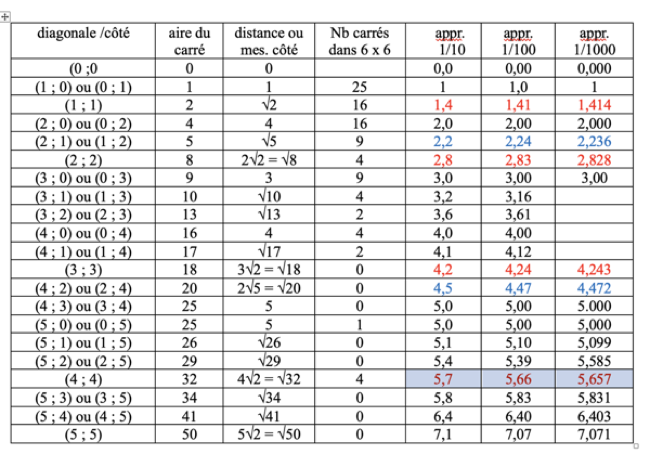
Tout ce qu'il faut savoir sur les longueurs de côtés de carrés dont les sommets sont sur les noeuds d'un quadrillage et leurs approximations décimales.
d) Pour ceux qui connaissent la relation de Pythagore, il y a là une belle occasion d'approcher une de ses démonstrations.
Bernard Anselmo, Roberto Battisti, Paola Bajorko, Clara Bisso, Brunella Brogi, Fabio Brunelli, Federica Curreli, Speranza Dettori, Florence Falguères, Lucia Grugnetti, François Jaquet, Silvia Mazzucco, Bice Perna, Luciana Rapposelli, Elsa Renna, Patrizia Sabatini, Rosanna Sanna, M. Agostina Satta, Cinzia Utzeri, Vincenza Vannucci (2024). Percorsi didattici per la geometria piana con problemi RMT / Parcours didactiques pour la géométrie plane par des problèmes RMT, Gazzetta n. 14, pp. 75-112.